Scroll to:
Patellar motion and dysfunction of its stabilizers in a biomechanical model of the knee joint
https://doi.org/10.47093/2218-7332.2024.15.1.47-60
Abstract
Aim. To develop a biomechanical model of the knee joint, including a detailed representation of the patellofemoral segment for the normal anatomy of bones, joints, ligaments and muscles, and study patellar movement during passive knee flexion.
Materials and methods. The architecture of the biomechanical model was developed using an open source software system for biomechanical modeling OpenSim. Patellofemoral joint with 6 degrees of freedom, patellar stabilizers – medial patellofemoral ligament (MPFL), medial patellotibial ligament (MPTL), lateral retinaculum (LR), and patellar contact surfaces (facets) were included in the model. Gmsh and Paraview were used to generate the contact surfaces. Simulations of knee passive flexion with consistent patellar stabilizers exclusion were carried out to identify their influence on patellar movement.
Results. The presented biomechanical model provides a detailed analysis of the normal dynamics of the patella and the role of different anatomical structures in its functioning and can be used for further experiments investigating of the patellar movement. The experiment involving all ligaments is consistent with the physiological norm. Disabling MPTL has minimal effects on patellar tilt and translation, which aligns with its small size. In contrast, deactivating MPFL results in increased lateral tilt and translation of the patella. Additionally, deactivation of LR components 1 and 2 induces more medial tilt and translation. Deactivating LR components 3 and 4 leads to further lateral translation and slight additional medial tilt.
Conclusion. Computational results show that all ligaments contribute to the normal movement of the patella. These findings highlight the importance of stabilizing structures in maintaining patellar stability during knee flexion.
List of abbreviation:
- LR – lateral retinaculum
- MPFL – medial patellofemoral ligament
- MPTL – medial patellotibial ligament
Patellofemoral pain is a prevalent type of knee pain that can affect individuals of various age groups, including adults, adolescents, and those who engage in physical activities. Clinical manifestations of impaired biomechanics in the femoro-patellar segment often lead to a significant reduction in the patients’ quality of life. Orthopedic pathologies of the patella make up a large proportion of all musculoskeletal system disorders.
The general population has an annual prevalence rate of 22.7% for patellofemoral pain, while adolescents have a higher prevalence rate of 28.9% [1]. The lateral patellar hyperpressure syndrome affects 7 to 15% of all patients with knee joint pathologies [2]. Pathologies of the patellofemoral joint are mainly observed in working individuals of young and middle age who lead an active lifestyle, making it socially significant [3][4]. In such cases, patellar displacement relative to the trochlear groove of the femur can be diagnosed [5]. This condition can be caused by congenital lateralization of the tuberosity of the tibia [6] and weakness of the medial vastus muscle of the thigh [7]. Lateral dislocation of the patella can also lead to cartilage degeneration or damage to the medial facet of the patella [8][9]. Lateral displacement can overload the lateral surface of the patella [10][11] and cause degradation of the articular cartilage [2]. Cartilage damage increases pressure on the subchondral bone and activates nociceptive fibers in the bone, causing pain [8].
Currently, surgical interventions for lateral patellar hyperpressure syndrome aim to: (1) correct the lateral position of the patella; (2) stabilize the patella; (3) increase compression of the medial thigh muscle group. Various arthroscopic techniques have been proposed for the treatment of hyperpressure syndrome [12].
Multiple studies present biomechanical models that contain the knee joint [13–17]. However, these models have a simplified representation of the patellofemoral joint, which is not suitable for investigations focused on this joint.
In model [18] during knee flexion, the patella moves along a specified trajectory, without contacting the femur surface, since the primary purpose of the model is to investigate the tibiofemoral joint and assess the loads that occur during its movement. Analysis of the potential use of this model for studying of patellar movement revealed several significant drawbacks, some of which are illustrated in Figure 1A-C: (1) the patella has only one degree of freedom during movement and has no contact with the femur during knee flexion; (2) ligaments and muscles intersect with bones during knee flexion; (3) patella size is unrealistically large in relation to the femur bone.
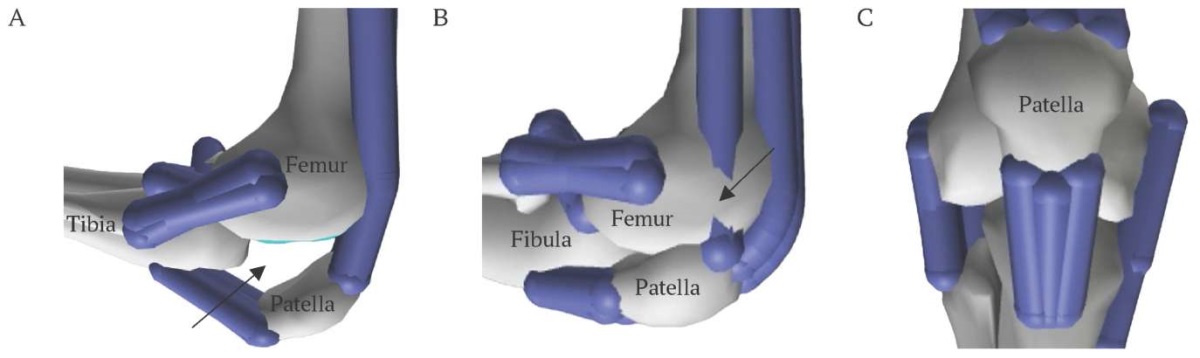
FIG. 1. Drawbacks of patella representation
(figures generated by the authors using model from [18]).
A. Patella has no contact to femur during knee flexion (arrow).
B. Some ligaments and muscles intersect bones during knee flexion (arrow).
C. Size of patella is unrealistically large in relation to femur.
РИС. 1. Недостатки представления надколенника
(рисунки получены авторами с использованием модели из [18]).
A. Надколенник не контактирует с бедренной костью при сгибании колена (стрелка).
B. Некоторые связки и мышцы пересекают кости во время сгибания колена (стрелка).
C. Размер надколенника является нереалистично большим по отношению к бедренной кости.
Note: gray color – bone structures; blue color – ligaments.
Примечание: серый цвет – костные структуры; синий – связки.
Development of accurate examination methods is necessary for modern medical diagnostics. Biomechanical models of the knee joint can be used as an additional tool for pathology evaluation. To our knowledge, there are no freely available models containing a detailed representation of the patellofemoral segment, nowadays.
The present study is aimed to create a biomechanical model of the knee joint, including a detailed representation of the patellofemoral segment for the normal anatomy of bones, joints, ligaments, and muscles, that enable studying of patellar movement during passive knee flexion.
MATERIALS AND METHODS
Model design was developed in collaboration with orthopedists from Sechenov University. Open source knee model [18] based on OpenSim platform [19][20] was chosen as a basis for constructing an advanced biomechanical model of the knee joint. The model consists of four solid bodies corresponding to bones (pelvis, femur, tibia, patella) and two joints: the articulation of the femur and tibia (tibiofemoral joint) and the articulation of the femur and patella (patellofemoral joint). The tibiofemoral joint is characterized by a joint with six degrees of freedom, while the patellofemoral joint has one degree of freedom in the model [18]. The main modifications made to the model [18] are detailed below.
Adding new ligaments
The knee joint model includes the patellar tendon, lateral collateral ligament, popliteal fibular ligament, medial collateral ligament, posterior cruciate ligament, anterior cruciate ligament, oblique popliteal ligament, medial patellofemoral ligament (MPFL), medial patellotibial ligament (MPTL), and lateral patellar retinaculum (LR). All ligaments, except for the MPFL, MPTL, and LR, are present in knee joint model [1]. Representations of patellar stabilizers MPFL, MPTL, and LR were added (Fig. 2). The MPFL is located on the inner side of the knee and connects the patella to the femur (Fig. 2A). The MPTL is also located on the inner side of the knee, connecting the patella to the tibia (Fig. 2B). The LR is located on the outer side of the knee and connects the patella to the femur, fibula, and tibia. The complex structure of the retinaculum [21] is represented in the model via four components (Fig. 2C).
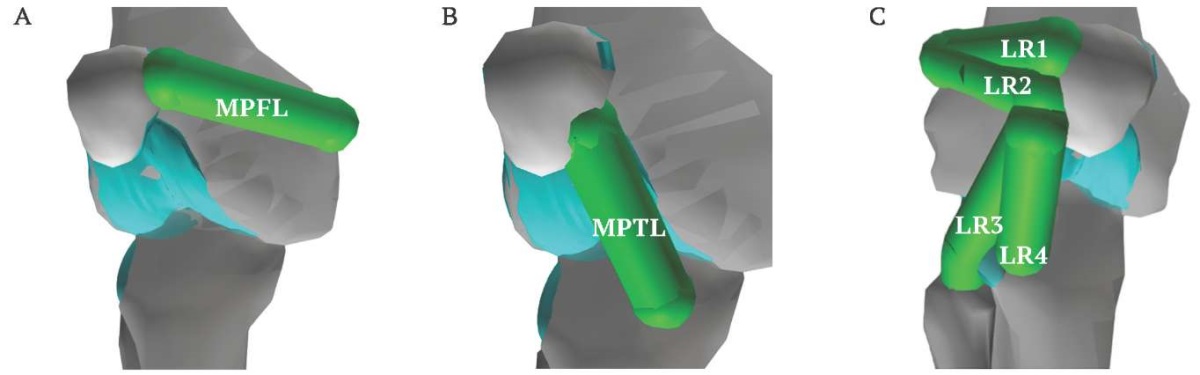
FIG. 2. Patellar stabilizers added to new biomechanical knee model.
A. Medial patellofemoral ligament (MPFL).
B. Medial patellotibial ligament (MPTL).
C. Lateral retinaculum (LR1–4).
РИС. 2. Стабилизаторы надколенника,
добавленные в новую биомеханическую модель.
A. Медиальная пателлофеморальная связка (MPFL).
B. Медиальная пателлотибиальная связка (MPTL).
C. Латеральный ретинакулум (LR1–4).
Various data on stiffness coefficient values and lengths of the MPFL and MPTL ligaments in a resting state can be found in published articles [22][23]. In agreement with orthopedists, stiffness coefficient values for these ligaments were adopted due to the anatomical similarity of the MPFL, MPTL, and superficial medial collateral ligament. The stiffness coefficient values for all ligaments were set to balance medial stabilizers during knee flexion for the case of healthy knee and were the same for each component and are provided in Supplementary materials (on the journal’s website, https://doi.org/10.47093/2218-7332.2024.15.1.47-60-table).
Adding new degrees of freedom
New possible directions of patellar movement were added: translations along the x, y, and z axes, and rotations around the y and x axes, respectively (Fig. 3). Rotation around the z-axis is defined as a linear function of a knee flexion angle. Changes in the patellar position over other directions during flexion occur due to various forces, including tension/compression of ligaments and muscles, contact interactions between articulating surfaces, and damping forces.
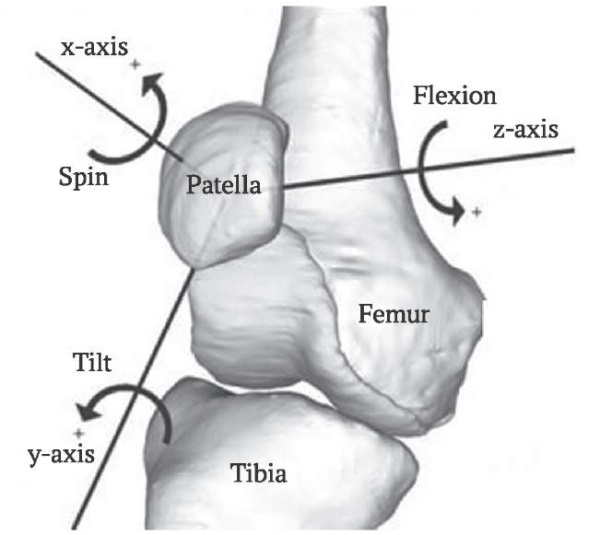
FIG. 3. Possible directions of patellar movement.
РИС. 3. Возможные направления движения надколенника.
Scaling of patella
To achieve realistic patellar sizes, scaling was applied to the surface mesh representing the patella from the model [18]. Relationships between patellar size and the distance between the lateral epicondyles of the femur were adopted. The scaling factor 0.65 was chosen along each of the x, y, and z axes. Modifying the surface mesh corresponding to the patella affects not only visualization of the patella in a graphical interface. The scaled patellar mesh was used to construct the contact surface, which shape influences directly the interaction between the patella and the femur.
Adding wrap objects
Possible intersections of ligaments or muscles and bones can significantly affect simulation results, as the forces generated in the ligaments and muscles depend on their relative elongation. In order to prevent intersection of ligaments or muscles with bones during knee flexion, wrap objects are included in the model. Wrap objects are shapes (e.g. spheres, ellipsoids, cylinders) that can be used to constrain ligaments and muscles. If the straight-line path connecting attachment points of a ligament or a muscle intersects a wrap object, a new path between these two points wrapping the object is calculated by one of the OpenSim algorithms. In this study, the “midpoint” method was used to determine a wrapping plane, which is the plane containing the ligament or muscle when wrapped around the ellipsoid. In the “midpoint” method we search for a point on the ellipsoid’s surface closest to the midpoint of the segment connecting origin and insertion points of the ligament or muscle. If the straight-line path between the attachment points is close to the ellipsoid’s center, the method becomes unstable. This feature of the algorithm imposes limitations on the choice of the position and size of the ellipsoid.
In this study wrap objects were added for the MPFL, MPTL, and LR ligaments. They were implemented as ellipsoids that approximate the surface of femoral and tibial condyles. The ellipsoids shape and position were manually adjusted using the graphical interface of OpenSim. Figure 4 demonstrates examples of two ellipsoids: the ellipsoid in Figure 4A approximates the lateral epicondyle of the femur, serving as a wrap object for the three components of the lateral retinaculum. The ellipsoid in Figure 4B is a wrap object for the fourth component of the lateral retinaculum, preventing its intersection with the tibia.
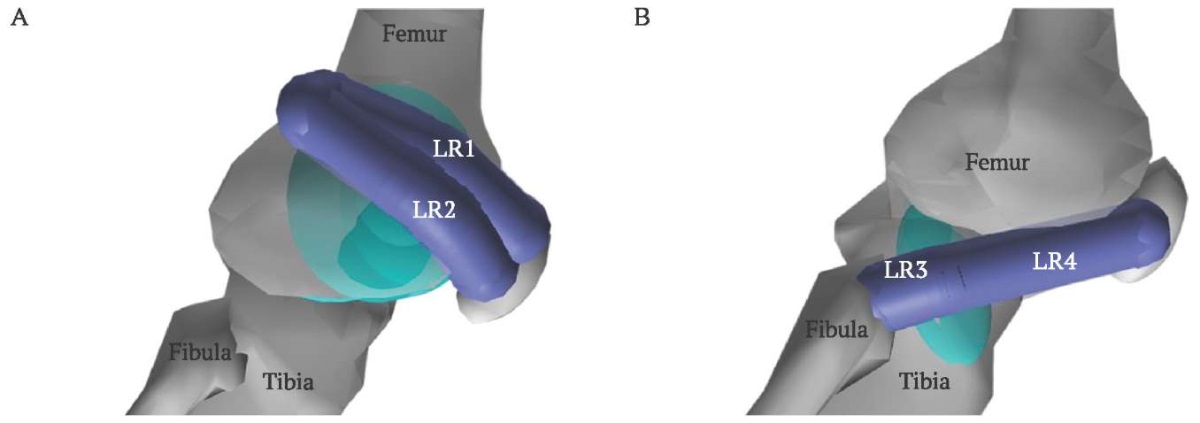
FIG. 4. Wrap ellipsoids.
A. The ellipsoid in the lateral condyle prevents intersection
of femur with retinaculum components 1 (LR1) and 2 (LR2).
B. The ellipsoid in tibia prevents intersection
of tibia with retinaculum components 3 (LR3) and 4 (LR4).
РИС. 4. Ограничивающие эллипсоиды.
A. Эллипсоид в латеральном мыщелке препятствует
проникновению компонентов ретинакулума 1 (LR1) и 2 (LR2)
в бедренную кость во время сгибания.
B. Эллипсоид в большеберцовой кости препятствует
проникновению компонентов ретинакулума 3 (LR3) и 4 (LR4)
в большеберцовую кость во время сгибания.
Adding patellar facets
To assess the load on different parts of the patellar cartilage surface, which covers it from the inside, 7 parts (facets) were selected on its surface:
- The medial (inner) facet of the patella is divided into 3 parts (upper, middle, lower);
- Lateral (outer) facet of the patella is divided into 3 parts (upper, middle, lower);
- Central facet of the patella (central longitudinal ridge).
To obtain surface meshes for facets, the OpenSim surface mesh for the patella was refined using Gmsh [24] (Fig. 5). On the refined mesh the triangles belonging to the facets can be selected so that they preserve the facet boundary.
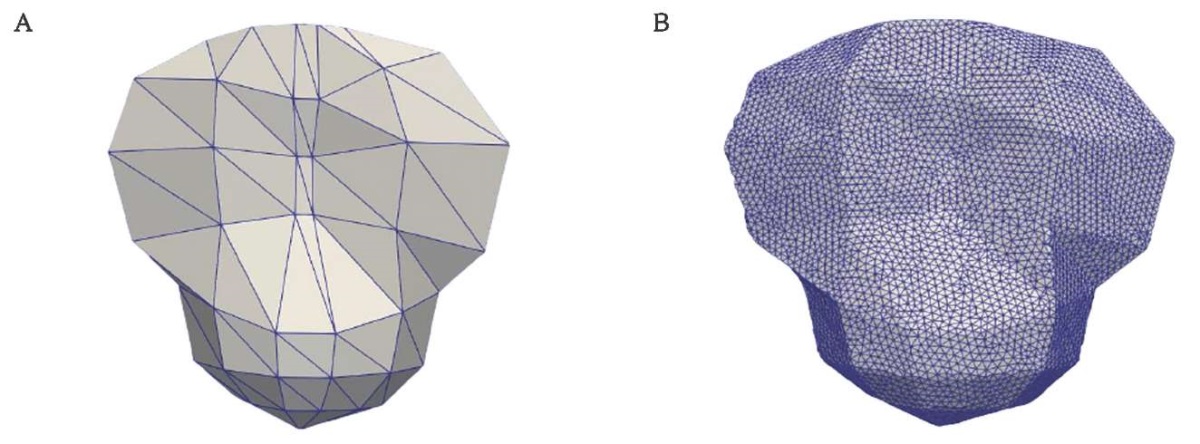
FIG. 5. Surface mesh for patella.
A. Initial patellar surface mesh provided by OpenSim.
B. Refined patellar surface mesh.
РИС. 5. Поверхностная сетка надколенника.
A. Исходная поверхностная сетка библиотеки OpenSim.
B. Измельченная поверхностная сетка.
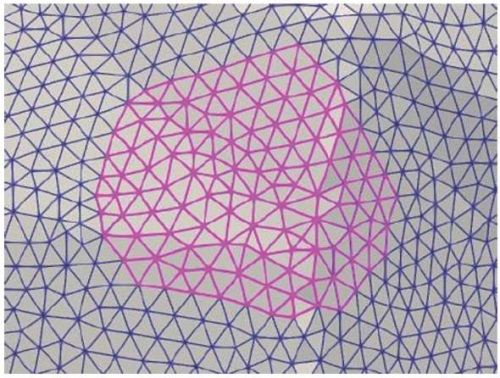
FIG. 6. Patellar facet triangles selected in Paraview.
РИС. 6. Треугольники поверхностной сетки,
соответствующие одной из фасеток, выделены с помощью программы Paraview.
Triangles of the facets were selected manually in Paraview [25] (Figs. 6, 7A). To imitate the volume of facets, mesh extrusion was performed using Gmsh [24] (Fig. 7B). The normals of all triangles were reoriented coherently after extrusion. The facets were scaled with a scale factor 0.65 to match the size of the scaled patella mesh.
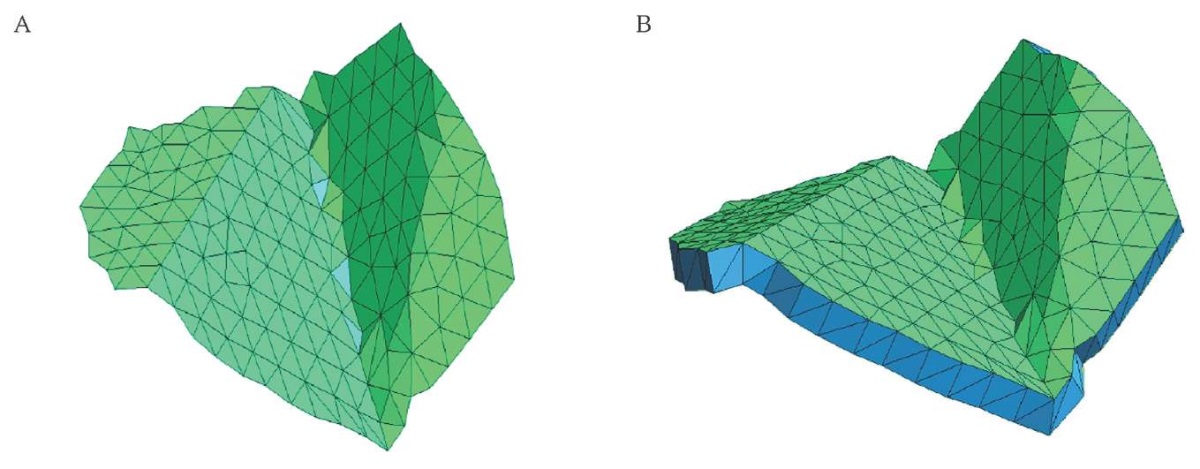
FIG. 7. Mesh of one of the facets.
A. Triangle mesh of the facet surface.
B. Extruded mesh.
РИС. 7. Сетка для одной из фасеток.
A. Треугольники поверхностной сетки для одной из фасеток.
B. Тетраэдральная сетка фасетки надколенника.
Generated meshes for patella facets (Fig. 8A) were included in the biomechanical OpenSim model as contact surfaces (Fig. 8B). The contact surfaces for the medial and lateral parts of trochlear groove contacting with the patella during knee flexion were present in the model [18].
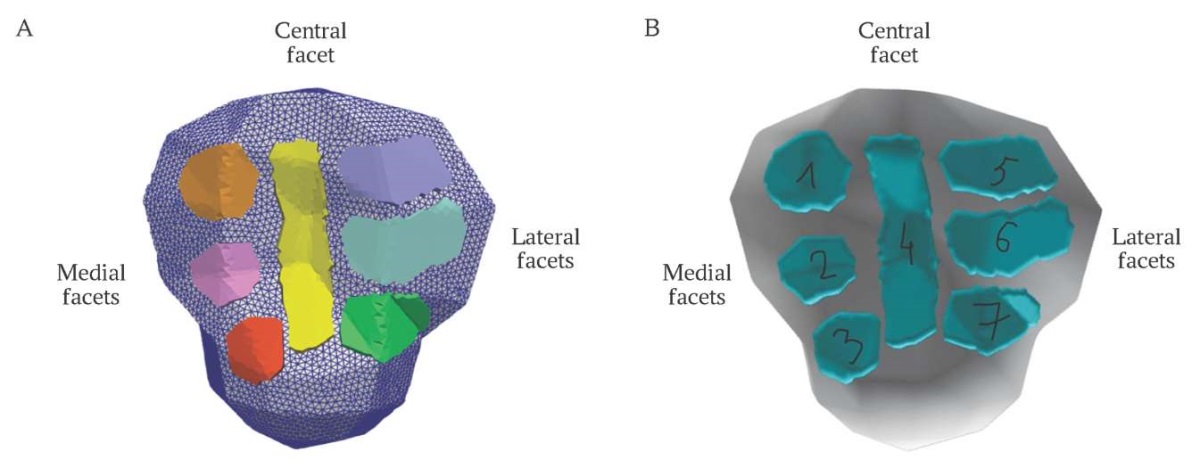
FIG. 8. Visualization of constructed facets.
A. Representation of surface meshes in Paraview, the facets are marked with color.
B. Patellar facets included in OpenSim model as contact surfaces:
1, 2, 3 are medial facets, 4 is central facet, 5, 6, 7 are lateral facets.
РИС. 8. Визуализация построенных фасеток.
A. Представление в виде сеток в Paraview, фасетки надколенника отмечены цветом.
B. Фасетки надколенника внедрены в модель в виде контактных поверхностей:
1, 2, 3 — медиальные фасетки, 4 – центральная, 5, 6, 7 — латеральные.
The elastic foundation contact model was used to implement contact interaction of each facet with lateral or medial femoral contact surface. The method employs meshes to represent contacting geometric surfaces of arbitrary complexity. The analysis of deformations and forces relies on a simplified elastic model [26]. For each contact element, a force consisting of three components is generated: stiffness, dissipation, and friction. Parameters were borrowed from the tibiofemoral contact implementation in model [18], where terms corresponding to friction were set to zero and the coefficient, which combines the individual dissipation properties of the two contacting materials, was set to 10. To prevent the passage of the patella through the femur during knee flexion, the value of the stiffness parameter was increased to 10¹². Adding of wrap objects to the model required adjustment of ligament resting length parameter, since the initial length of some ligaments has increased.
Model evaluation
The model design presented above contains all the functional elements for patellofemoral joint investigation. To analyze the trajectory of the patellar movement, the load distribution on its surface, and the functioning of the stabilizers, modeling of passive knee flexion was performed.
The entire model is presented as a system of rigid bodies to which certain forces are applied. The position of the bodies relative to each other and the laboratory coordinate system is described by the vector of generalized coordinates q, the velocities of the bodies relative to each other and the laboratory coordinate system are given by the vector of generalized velocities q̇. The state of the system at some point in time t is given by a system of equations in generalized coordinates. To compute generalized coordinates and generalized velocities change over time depending on the forces applied to bodies and load distribution on the articular surfaces of the patella during passive knee flexion, Opensim Forward dynamics tool can be used. The tool is implemented using a mathematical model that includes the following main elements:
- Model of the human body, which is described by a system of differential equations of motion, taking into account the forces and moments acting on each joint;
- Muscle ligament model, which allows to determine the forces and moments generated by muscle ligament during movement;
- Contact model, which describes the interaction between the bodies;
- Control model that determines the activation of muscle fibers and coordinates their contraction to perform a given movement.
The state of a model refers to the complete set of model variables defined at a specific moment in time. Model dynamics describes the model’s progression from one state to another over time. The simulation involves integrating the dynamic equations of the musculoskeletal model, starting from an initial state, corresponding to full extension of the knee joint. To integrate numerically the dynamical equations, a 5th-order Runge-Kutta-Feldberg integrator is used.
In order to compute ligaments tensions, patellar trajectory and load distribution on the articular surfaces of the patella during passive knee flexion, we use OpenSim Forward dynamics tool. Passive knee flexion was simulated over a 20-second time interval.
The following experiments were carried out:
- all ligaments are included;
- MPFL is disabled;
- MPTL is disabled;
- components of LR 1 and 2 are disabled;
- components of LR 3 and 4 are disabled.
RESULTS
The first experiment corresponds to the physiological norm, experiments 2–5 imitate disfunction of patellar stabilizers. The tensions generated in the patellar stabilizers, contact forces on patellar facets and changes in patellar trajectory were considered. The plots in Figure 9 illustrate changes in tensions generated by the ligaments during knee flexion. The tensions of retinaculum component 4 occur only in experiment 4 (disabled LR 1, 2). Other ligaments generate tensions in every run, the tensions depend on the run parameters.
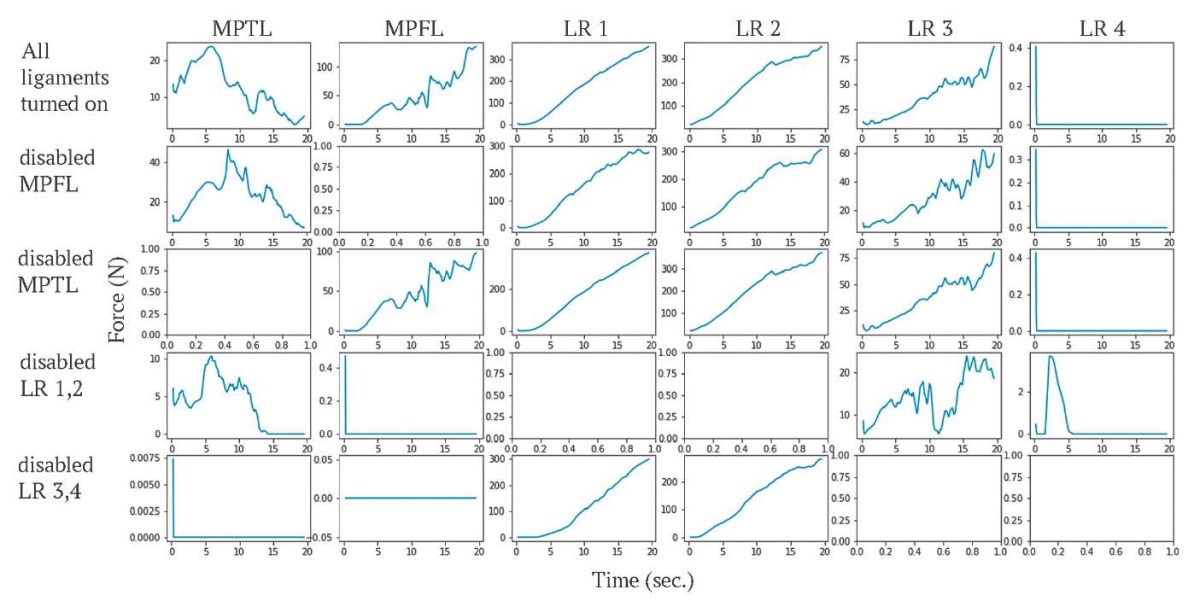
FIG. 9. Forces generated by the ligaments during knee flexion,
the unit of force is newton.
РИС. 9. График изменения сил (в ньютонах), генерируемых связками,
во время сгибания колена.
Note: MPFL – medial patellofemoral ligament;
MPTL – medial patellotibial ligament; LR – lateral patellar retinaculum.
Примечание: MPFL – medial patellofemoral ligament,
медиальная пателлофеморальная связка;
MPTL – medial patellotibial ligament, медиальная пателлотибиальная связка;
LR – lateral patellar retinaculum, латеральный ретинакулум.
Contact forces on the facets are shown in Figure 10. Forces occur on the medial facets only in experiments 4–5 (disabled components of LR). Forces are applied to the lateral facets in each run. There is no force acting on the central facet.
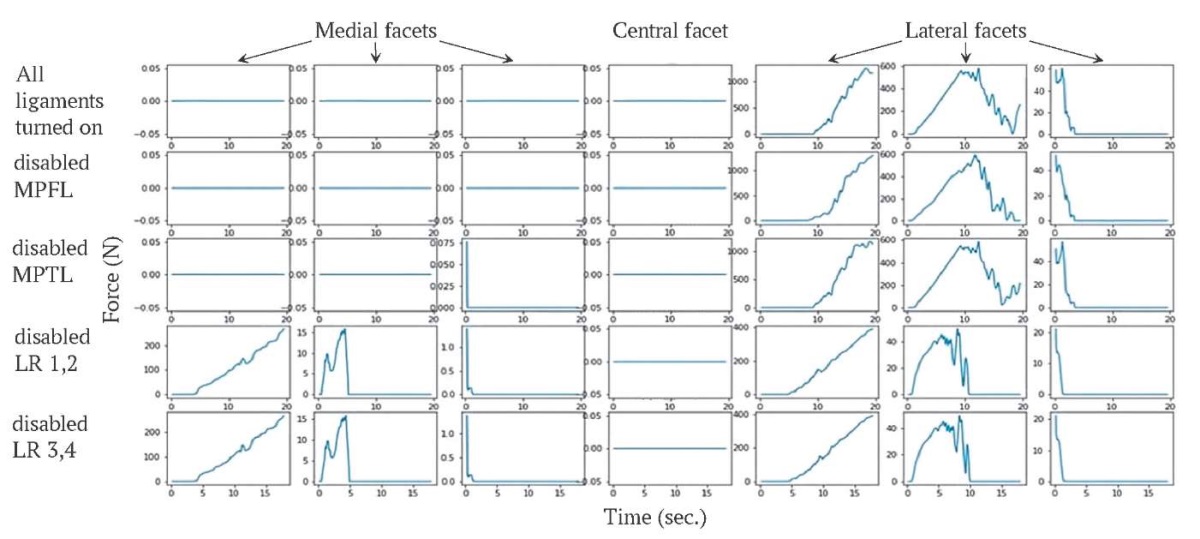
FIG. 10. Forces acting on the facets during knee flexion,
the unit of force is newton.
РИС. 10. График изменения сил (в ньютонах), действующих на фасетки,
во время сгибания колена.
Note: MPFL – medial patellofemoral ligament;
MPTL – medial patellotibial ligament; LR – lateral patellar retinaculum.
Примечание: MPFL – medial patellofemoral ligament,
медиальная пателлофеморальная связка;
MPTL – medial patellotibial ligament, медиальная пателлотибиальная связка;
LR – lateral patellar retinaculum, латеральный ретинакулум.
Changes in patellar tilt and translation due to ligament disabling are demonstrated in Figures 11A–D and Figures 12A–D, respectively. The disabling of MPTL has almost no influence on patellar tilt and translation. The result is consistent with the small size of MPTL. The impact of MPFL on patella trajectory is stronger, since MPFL deactivation leads to additional lateral tilt and lateral translation. Deactivation of LR 1 and 2 causes additional medial tilt and medial translation. Deactivation of retinaculum components 3 and 4 causes additional lateral translation and slight additional medial tilt.
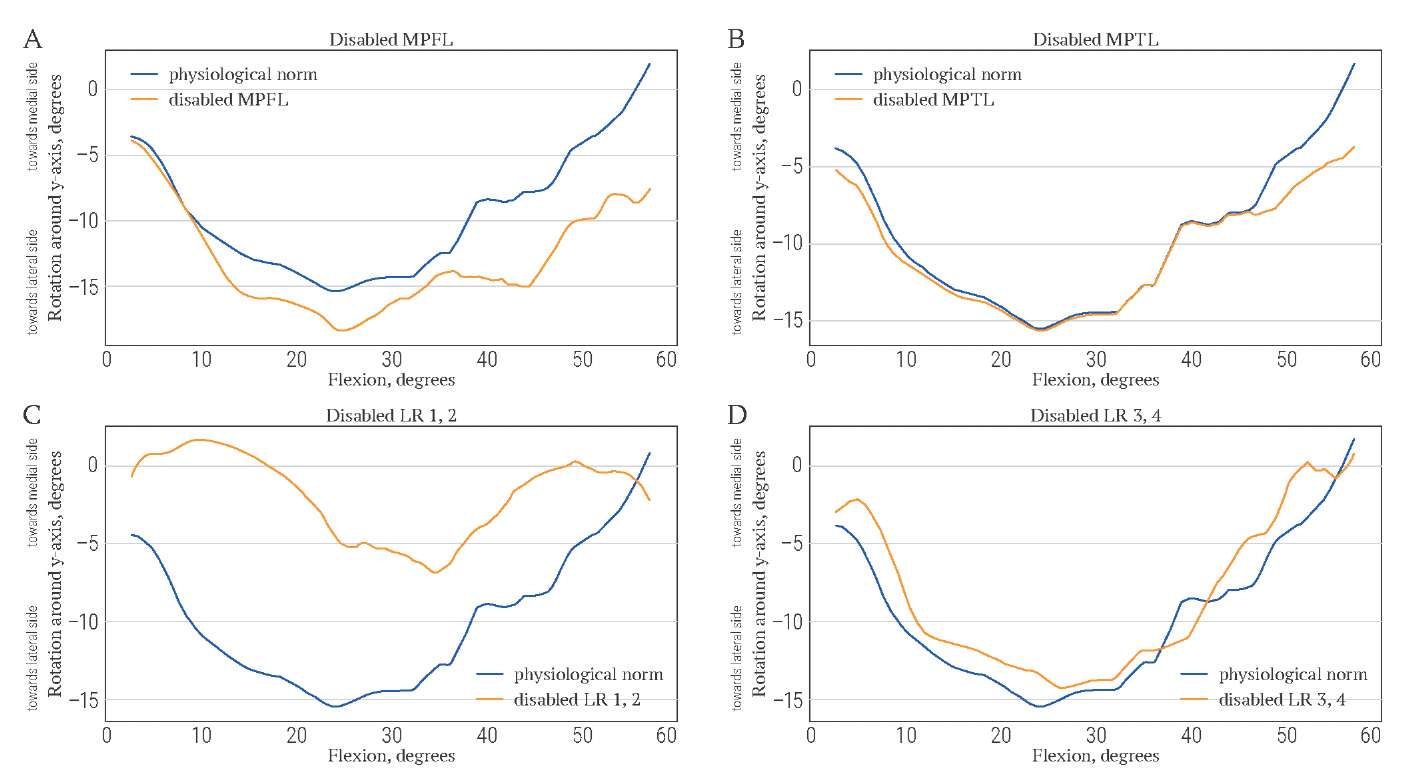
FIG. 11. Lateral-medial tilt of patella (in degrees) during knee flexion (in degrees)
when stabilizers are disabled.
РИС. 11. Латерально-медиальный наклон надколенника (в градусах)
во время сгибания колена (в градусах)
при отключении стабилизаторов надколенника.
Note: MPFL – medial patellofemoral ligament;
MPTL – medial patellotibial ligament; LR – lateral patellar retinaculum.
Примечание: MPFL – medial patellofemoral ligament,
медиальная пателлофеморальная связка;
MPTL – medial patellotibial ligament, медиальная пателлотибиальная связка;
LR – lateral patellar retinaculum, латеральный ретинакулум.
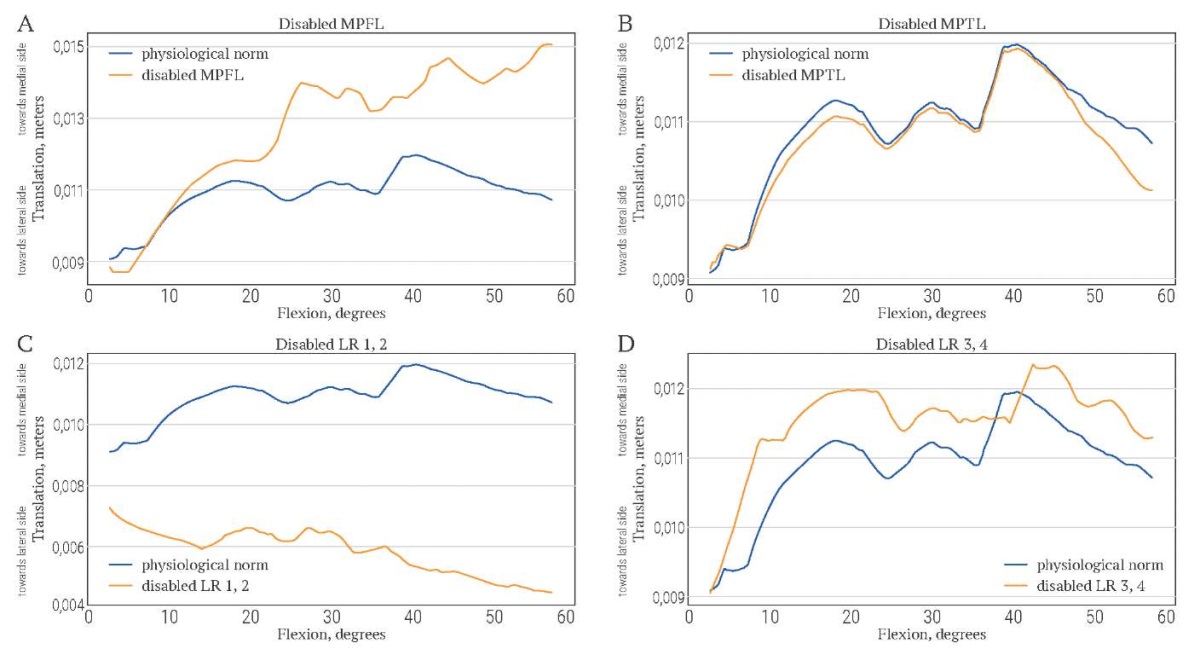
FIG. 12. Lateral-medial translation of patella (in meters) during knee flexion (in degrees)
when stabilizers are disabled.
РИС. 12. Латерально-медиальное смещение надколенника (в метрах)
во время сгибания колена (в градусах)
при отключении стабилизаторов надколенника.
Note: MPFL – medial patellofemoral ligament;
MPTL – medial patellotibial ligament; LR – lateral patellar retinaculum.
Примечание: MPFL – medial patellofemoral ligament,
медиальная пателлофеморальная связка;
MPTL – medial patellotibial ligament, медиальная пателлотибиальная связка;
LR – lateral patellar retinaculum, латеральный ретинакулум.
DICSUSSION
The biomechanical model for patellar motion studying was developed. Simulations of passive knee flexion were performed. Experiments with patellar stabilizers deactivation were carried out. The contemporary literature still lacks studies on modeling various pathological conditions of the knee joint capsuloligamentous apparatus work. The results of our experiment on the biomechanical model of the knee joint showed coincidence of patellar movements with clinical experience when its ligamentous apparatus is damaged [27–31].
In this paper, we presented results for passive knee joint flexion modeling. However, the model developed in this study can also be used to analyze knee joint function during movement. Since the proposed model design has been implemented for the standard bone geometries provided by OpenSim, it can be easily integrated into other open-access OpenSim models containing the knee joint, e.g. into the OpenSim “Full Body Model for use in Dynamic Simulations of Human Gait” [13]. The detailed representation of the knee joint allows for the analysis of patellar stabilizer tensions and contact forces between the patella and femur during the gait cycle.
This research has significant implications for understanding injuries and diseases that affect the supporting structures of the patella. By gaining insight into these changes, medical professionals will be better equipped for choosing appropriate treatment strategies and rehabilitation plans for patients. Additionally, the computational biomechanical model opens up new possibilities for the treatment of patellar pathologies. It provides a platform for further research and development of innovative approaches to address these conditions.
Model personalization is one of the most important perspectives of this project. However, for its application in clinical practice, automation of the model generation stages is necessary. Relatively large simulation time (3–4 hours) is also an important limitation for the application of the model in clinical practice.
The development of an accurate biomechanical model, enabling experiments with ligament injuries, serves as a prerequisite for the creation of a novel diagnostic tool to assess the extent of damage and devise a treatment strategy for the patient.
CONCLUSION
The presented biomechanical model provides a detailed analysis of the normal dynamics of the patella and the role of different anatomical structures in its functioning. Besides this, we analyzed via series of computer experiments complex biomechanical changes that occur when the patellar stabilizers are compromised. In summary, this work has provided a comprehensive understanding of the normal functioning of the patella and the consequences of its destabilization. It has practical implications for medical professionals and offers new opportunities for improving the treatment of patellar pathologies. The model is freely available for download at https://simtk.org/projects/kneepatfemjoint
AUTHOR CONTRIBUTION
Alexandra S. Yurova developed the model and performed project supervision. Alexandra S. Tyagunova adjusted model parameters, constructed patellar facets and carried out experiments. Fedor B. Loginov carried out experiments and performed visualization of results. Yuri V. Vassilevski managed and coordinated responsibility for the research activity planning and execution, acquired the financial support for the project leading to this publication. Eugene B. Kalinsky and Alexey V. Lychagin formulated the problem and proposed some concepts of model design. Elena V. Larina tested model components, Natalia V. Gorohova and Kirill A. Devyatyarov maintained research data for initial use and later reuse. Oleg N. Bogdanov, Ilya B. Kovalenko and Ksenia V. Chesnokova performed results analysis. Maxim A. Dergachev, Eugene Yu. Mychka and Oleg N. Kosukhin prepared the initial draft of the paper. All authors participated in the discussion and editing of the work. All authors approved the final version of the article.
ВКЛАД АВТОРОВ
А.С. Юрова занималась разработкой модели и руководством проектом. А.С. Тягунова настраивала параметры модели, строила фасетки надколенника и проводила эксперименты. Ф.Б. Логинов проводил эксперименты и визуализацию результатов. Ю.В. Василевский координировал выполнение исследовательской деятельности, обеспечил финансовую поддержку проекта. Е.Б. Калинский и А.В. Лычагин сформулировали постановку задачи и предложили некоторые концепции архитектуры модели. Е.В. Ларина тестировала компоненты модели, Н.В. Горохова и К.А. Девятьяров осуществляли поддержку исследовательских данных. О.Н. Богданов, И.Б. Коваленко и К.В. Чеснокова проводили анализ результатов. М.А. Дергачев, Е.Ю. Мычка и О.Н. Косухин подготовили первоначальный текст статьи. Все авторы участвовали в обсуждении и редактировании работы. Все авторы одобрили окончательную версию статьи.
Ethics statements. No ethical approval by the local Ethics Committee was required since the study was not conducted on humans or laboratory animals.
Data availability statement. The model is freely available for download at https://simtk.org/projects/kneepatfemjoint
Conflict of interests. The authors declare that there is no conflict of interests.
Financial support. The study was supported by the Russian Science Foundation, project no. 21-71-300231.
Соответствие принципам этики. Утверждение протокола Локальным этическим комитетом не требовалось, так как исследование не проводилось на людях или лабораторных животных.
Политика открытых данных. Модель доступна в открытом доступе: https://simtk.org/projects/kneepatfemjoint
Конфликт интересов. Авторы заявляют об отсутствии конфликта интересов.
Финансирование. Исследование выполнено за счет гранта Российского научного фонда № 21-71-300232.
1. https://rscf.ru/prjcard_int?21-71-30023&ysclid=lu4efmes8g254850327
2. https://rscf.ru/prjcard_int?21-71-30023&ysclid=lu4efmes8g254850327
References
1. Smith B.E., Selfe J., Thacker D., et al. Incidence and prevalence of patellofemoral pain: A systematic review and meta-analysis. PLoS One. 2018 Jan 11; 13(1): e0190892. https://doi.org/10.1371/journal.pone.0190892. PMID: 29324820; PMCID: PMC5764329
2. Kamat Y., Prabhakar A., Shetty V., Naik A. Patellofemoral joint degeneration: A review of current management. J Clin Orthop Trauma. 2021 Nov 13; 24: 101690. https://doi.org/10.1016/j.jcot.2021.101690. PMID: 34900577; PMCID: PMC8636808
3. van Leeuwen G.J., de Schepper E.I.T., Bindels P.J.E., et al. Patellofemoral pain in general practice: the incidence and management. Fam Pract. 2023 Nov 23; 40(4): 589–595. https://doi.org/10.1093/fampra/cmad087. PMID: 37669000; PMCID: PMC10667070
4. Ferreira C.L., Oliveira Barroso F., Torricelli D., et al. Muscle synergies analysis shows altered neural strategies in women with patellofemoral pain during walking. PLoS One. 2023 Oct 5; 18(10): e0292464. https://doi.org/10.1371/journal.pone.0292464. PMID: 37796922; PMCID: PMC10553307
5. Barroso Rosa S., Grant A., McEwen P. Patient-reported outcome measures for patellofemoral disorders: a systematic review. Arch Orthop Trauma Surg. 2023 Jul; 143(7): 3919–3927. https://doi.org/10.1007/s00402-022-04663-3. Epub 2022 Oct 19. PMID: 36260119
6. Talbot S., Zordan R., Bennett K., et al. Quadriceps tendon malalignment is an independent anatomical deformity which is the primary abnormality associated with lateral facet patellofemoral joint osteoarthritis. Knee Surg Sports Traumatol Arthrosc. 2023 Dec; 31(12): 5950–5961. https://doi.org/10.1007/s00167-023-07661-z. Epub 2023 Nov 21. PMID: 37989778
7. Li Z., Huang C., Leung K.L., et al. Strength and passive stiffness of the quadriceps are associated with patellar alignment in older adults with knee pain. Clin Biomech (Bristol, Avon). 2023 Dec; 110: 106131. https://doi.org/10.1016/j.clinbiomech.2023.106131. Epub 2023 Oct 24. PMID: 37925827
8. Brenneis M., Junker M., Sohn R., et al. Patellar malalignment correlates with increased pain and increased synovial stress hormone levels-A cross-sectional study. PLoS One. 2023 Jul 27; 18(7): e0289298. https://doi.org/10.1371/journal.pone.0289298. PMID: 37498905; PMCID: PMC10374142
9. Elias J.J., Cosgarea A.J., Tanaka M.J. Adding tibial tuberosity medialization to medial patellofemoral ligament reconstruction reduces lateral patellar maltracking during multidirectional motion in a computational simulation model. Arthrosc Sports Med Rehabil. 2023 Jul 10; 5(4): 100753. https://doi.org/10.1016/j.asmr.2023.100753. PMID: 37645404; PMCID: PMC10461214
10. Little R.D., Smith S.E., Cicuttini F.M., et al. Association between increased signal intensity at the proximal patellar tendon and patellofemoral geometry in community-based asymptomatic middle-aged adults: a cross-sectional study. BMC Musculoskelet Disord. 2020 Aug 22; 21(1): 571. https://doi.org/10.1186/s12891-020-03589-4. PMID: 32828128; PMCID: PMC7443287
11. Hashimoto Y., Nishino K., Tomohiro T., et al. The remaining parameters of patellar instability could be affected for osteoarthritic change after medial patellofemoral ligament reconstruction with or without anteromedialization of the tibial tubercle osteotomy for patellar instability: a retrospective cohort study. BMC Musculoskelet Disord. 2023 Jan 23; 24(1): 56. https://doi.org/10.1186/s12891-022-06100-3. PMID: 36683021; PMCID: PMC9869604
12. Cerciello S., Lustig S., Costanzo G., Neyret P. Medial retinaculum reefi ng for the treatment for patellar instability. Knee Surg Sports Traumatol Arthrosc. 2014 Oct; 22(10): 2505–2512. https://doi.org/10.1007/s00167-014-3171-6. Epub 2014 Jul 25. PMID: 25059335
13. Rajagopal A., Dembia C.L., DeMers M.S., et al. Full-body musculoskeletal model for muscle-driven simulation of human gait. IEEE Trans Biomed Eng. 2016 Oct; 63(10): 2068–2079. https://doi.org/10.1109/TBME.2016.2586891. Epub 2016 Jul 7. PMID: 27392337; PMCID: PMC5507211
14. Bedo B.L.S, Catelli D.S., Lamontagne M., Santiago P.R.P. A custom musculoskeletal model for estimation of medial and lateral tibiofemoral contact forces during tasks with high knee and hip fl exions. Comput Methods Biomech Biomed Engin. 2020 Aug; 23(10): 658–663. https://doi.org/10.1080/10255842.2020.175766 2. Epub 2020 May 12. PMID: 32393120
15. Saxby D.J., Modenese L., Bryant A.L., et al. Tibiofemoral contact forces during walking, running and sidestepping. Gait Posture. 2016 Sep; 49: 78–85. https://doi.org/10.1016/j.gaitpost.2016.06.014. Epub 2016 Jun 21. PMID: 27391249
16. Lee M.R., Hicks J.L., Wren T.A.L., Delp S.L. Independently ambulatory children with spina bifi da experience near-typical knee and ankle joint moments and forces during walking. Gait Posture. 2023 Jan; 99: 1–8. https://doi.org/10.1016/j.gaitpost.2022.10.010. Epub 2022 Oct 18. PMID: 36283301; PMCID: PMC9772073
17. Adouni M., Alkhatib F., Gouissem A., Faisal T.R. Knee joint biomechanics and cartilage damage prediction during landing: A hybrid MD-FE-musculoskeletal modeling. PLoS One. 2023 Aug 3; 18(8): e0287479. https://doi.org/10.1371/journal.pone.0287479. PMID: 37535559; PMCID: PMC10399834
18. Schmitz A., Piovesan D. Development of an open-source, discrete element knee model. IEEE Trans Biomed Eng. 2016 Oct; 63(10): 2056–2067. https://doi.org/10.1109/TBME.2016.2585926. Epub 2016 Jun 28. PMID: 27362757
19. Seth A., Hicks J.L, Uchida T.K., et al. OpenSim: Simulating musculoskeletal dynamics and neuromuscular control to study human and animal movement. PLoS Comput Biol. 2018 Jul 26; 14(7): e1006223. https://doi.org/10.1371/journal.pcbi.1006223. PMID: 30048444; PMCID: PMC6061994
20. Delp S.L., Anderson F.C., Arnold A.S., et al. OpenSim: opensource software to create and analyze dynamic simulations of movement. IEEE Trans Biomed Eng. 2007 Nov; 54(11): 1940–1950. https://doi.org/10.1109/TBME.2007.901024. PMID: 18018689
21. Hayden D.J., Doshi C., Parikh S.N. Lateral patellar retinaculum Z-lengthening. Arthrosc Tech. 2021 Jun 28; 10(7): e1883–e1887. https://doi.org/10.1016/j.eats.2021.04.010. PMID: 34336590; PMCID: PMC8322702
22. Frodl A., Lange T., Siegel M., et al. Individual infl uence of trochlear dysplasia on patellofemoral kinematics after isolated MPFL reconstruction. J Pers Med. 2022 Dec 12; 12(12): 2049. https://doi.org/10.3390/jpm12122049. PMID: 36556269; PMCID: PMC9786691
23. Abbaszadeh A., Saeedi M., Hoveidaei A.H., et al. Combined medial patellofemoral ligament and medial patellotibial ligament reconstruction in recurrent patellar instability: A systematic review and meta-analysis. World J Clin Cases. 2023 Jul 6; 11(19): 4625–4634. https://doi.org/10.12998/wjcc.v11.i19.4625. PMID: 37469731; PMCID: PMC10353511
24. Geuzaine C., Remacle J.-F. Gmsh: A 3-D fi nite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Meth. Engng., 2009; 79: 1309–1331. https://doi.org/10.1002/nme.2579
25. Ahrens J., Geveci B., Law C. 36 – ParaView: An end-user tool for large data visualization. Editors: Charles D. Hansen, Chris R. Johnson. The visualization handbook. Butterworth-Heinemann, 2005, 717–731. ISBN 9780123875822. https://doi.org/10.1016/B978-012387582-2/50038-1
26. Sherman M.A., Seth A., Delp S.L. Simbody: multibody dynamics for biomedical research. Procedia IUTAM. 2011; 2: 241–261. https://doi.org/10.1016/j.piutam.2011.04.023. PMID: 25866705; PMCID: PMC4390141
27. Loudon J.K. Biomechanics and pathomechanics of the patellofemoral joint. Int J Sports Phys Ther. 2016 Dec; 11(6): 820–830. PMID: 27904787; PMCID: PMC5095937
28. Mizu-Uchi H., Ma Y., Ishibashi S., et al. Tibial sagittal and rotational alignment reduce patellofemoral stresses in posterior stabilized total knee arthroplasty. Sci Rep. 2022 Jul 19; 12(1): 12319. https://doi.org/10.1038/s41598-022-15759-6. PMID: 35854017; PMCID: PMC9296446
29. Yu Z., Yao J., Wang X., et al. Research methods and progress of patellofemoral joint kinematics: a review. J Healthc Eng. 2019 Mar 24; 2019: 9159267. https://doi.org/10.1155/2019/9159267. PMID: 31019669; PMCID: PMC6451817
30. Tan S.H.S., Ngiam E.H.K., Lim J.Y., et al. Surgical management of patella alta in patellofemoral instability: a systematic review and meta-analysis. Orthop J Sports Med. 2021 Apr 21; 9(4): 2325967121999642. https://doi.org/10.1177/2325967121999642. PMID: 33997063; PMCID: PMC8072862
31. Baryeh K., Getachew F. Patella dislocation: an overview. Br J Hosp Med (Lond). 2021 Aug 2; 82(8): 1–10. https://doi.org/10.12968/hmed.2020.0429. Epub 2021 Aug 4. PMID: 34431342
About the Authors
A. S. YurovaRussian Federation
Alexandra S. Yurova, Cand. of Sci. (Physics and Mathematics), researcher
8, Gubkin str., Moscow, 119333
A. I. Tyagunova
Russian Federation
Alexandra I. Tyagunova, student
8/2, Trubetskaya str., Moscow, 119048
1, Olympic pr., Sochi, 354340
F. B. Loginov
Russian Federation
Fedor B. Loginov, student
8/2, Trubetskaya str., Moscow, 119048
Yu. V. Vassilevski
Russian Federation
Yuri V. Vassilevski, Dr. of Sci. (Physics and Mathematics), Deputy Director for science; Head of Mathematics, Mechanics and Mathematical Modelling Department; Head of Department "Mathematical modeling in biomedicine and geophysics", Scientifi c Center for Information Technologies and Artifi cial Intelligence
8, Gubkin str., Moscow, 119333
8/2, Trubetskaya str., Moscow, 119048
1, Olympic pr., Sochi, 354340
A. V. Lychagin
Russian Federation
Alexey V. Lychagin, Dr. of Sci. (Medicine), Head of Traumatology, Orthopedics and Disaster Medicine Department
8/2, Trubetskaya str., Moscow, 119048
E. B. Kalinsky
Russian Federation
Eugene B. Kalinsky, Dr. of Sci. (Medicine), Associate Professor, Traumatology, Orthopedics and Disaster Medicine Department
8/2, Trubetskaya str., Moscow, 119048
E. V. Larina
Russian Federation
Elena V. Larina, Cand. of Sci. (Physics and Mathematics), Associate Professor, Mathematics, Mechanics and Mathematical Modelling Department
8/2, Trubetskaya str., Moscow, 119048
N. V. Gorohova
Russian Federation
Natalia V. Gorohova, Cand. of Sci. (Physics and Mathematics), Associate Professor, Mathematics, Mechanics and Mathematical Modelling Department
8/2, Trubetskaya str., Moscow, 119048
K. A. Devyatyarov
Russian Federation
Kirill A. Devyatyarov, Assistant Professor, Mathematics, Mechanics and Mathematical Modelling Department
8/2, Trubetskaya str., Moscow, 119048
O. N. Bogdanov
Russian Federation
Oleg N. Bogdanov, Cand. of Sci. (Physics and Mathematics), Associate Professor, Mathematics, Mechanics and Mathematical Modelling Department
8/2, Trubetskaya str., Moscow, 119048
I. B. Kovalenko
Russian Federation
Ilya B. Kovalenko, Dr. of Sci. (Physics and Mathematics), Professor, Mathematics, Mechanics and Mathematical Modelling Department
8/2, Trubetskaya str., Moscow, 119048
K. V. Chesnokova
Russian Federation
Ksenia V. Chesnokova, Cand. of Sci. (Physics and Mathematics), Associate Professor, Mathematics, Mechanics and Mathematical Modelling Department
8/2, Trubetskaya str., Moscow, 119048
M. A. Dergachev
Russian Federation
Maxim A. Dergachev, Senior Lecturer, Mathematics, Mechanics and Mathematical Modelling Department
8/2, Trubetskaya str., Moscow, 119048
E. Yu. Mychka
Russian Federation
Eugene Yu. Mychka, Cand. of Sci. (Physics and Mathematics), Associate Professor, Mathematics, Mechanics and Mathematical Modelling Department
8/2, Trubetskaya str., Moscow, 119048
O. N. Kosukhin
Russian Federation
Oleg N. Kosukhin, Cand. of Sci. (Physics and Mathematics), Associate Professor, Mathematics, Mechanics and Mathematical Modelling Department
8/2, Trubetskaya str., Moscow, 119048
Supplementary files

|
1. Table. The stiffness coefficient values for the ligaments included in the model | |
| Subject | ||
| Type | Исследовательские инструменты | |
Download
(755KB)
|
Indexing metadata ▾ | |