Перейти к:
Базовые аспекты мета-анализа. Часть 2
https://doi.org/10.47093/2218-7332.2024.15.2.4-12
Аннотация
Мета-анализ объединяет результаты нескольких научных исследований для получения обобщенной количественной оценки величины эффекта, для сравнения результатов нескольких исследований, выявления в них закономерностей и возможных источников разногласий. Поскольку оригинальные научные исследования проводятся разными коллективами авторов, с разными пациентами, в разные временные промежутки, по разным протоколам и клиническим рекомендациям, все перечисленные факторы могут оказывать влияние на результаты отдельно взятого исследования, обусловливая статистическую гетерогенность. Мета- анализы занимают высшую степень достоверности в концепции доказательной медицины, так как позволяют учитывать влияние множества вмешивающихся факторов и публикационных смещений на истинный размер эффекта. Понимание возможных источников ошибочных заключений в исследованиях позволит научным сотрудникам критически относиться к интерпретации результатов и корректно планировать собственные эксперименты. В настоящей статье читатель познакомится с методами выявления и количественной оценки скрытой гетерогенности, такими как анализ подгрупп и метарегрессионный анализ. Кроме того, читатель научится производить расчет размера эффекта в исследованиях, математически и графически оценивать публикационные смещения, а также учитывать эту оценку при проведении мета-анализа в общей усредненной оценке размера эффекта.
Ключевые слова
В первой части цикла статей, посвященных базовым аспектам мета-анализа, рассмотрено само понятие мета-анализа и представлены основные рекомендации, которыми необходимо руководствоваться при его проведении [1]. Мы узнали, как применять графики риска смещений для оценки наличия смещений в исследованиях; выяснили, чем может быть обусловлена гетерогенность исследований, и рассмотрели способы ее вычисления. Также мы детально обсудили различные типы моделей, позволяющие обобщить результаты исследований, и способы расчета весов исследования в общей усредненной оценке размера эффекта. Кроме того, мы затронули аналитический метод анализа чувствительности – метод leave-one-out и продемонстрировали графическое представление такой оценки, а также представили основную диаграмму для отображения результатов мета-анализа – форест-диаграмму (forest plot).
Включенные в мета-анализ оригинальные исследования могут различаться, поскольку проводились разными коллективами, с разными пациентами, в разные временные промежутки. С целью учета подобных различий между клиническими исследованиями введено понятие гетерогенности, оценка и учет которой важны для объективного количественного обобщения результатов. Разнообразие характеристик пациентов, медицинских вмешательств и исходов считают клинической гетерогенностью. Вариабельность дизайна исследований, методик оценки исходов и различных единиц измерения обозначают методологической гетерогенностью. Оба вышеуказанных вида гетерогенности приводят к появлению статистической гетерогенности, связанной с различиями в оценке размера эффекта. При дальнейшем рассмотрении гетерогенности в текущей статье мы будем считать, что методологическая и клиническая гетерогенность сведены к минимуму, а имеющаяся статистическая гетерогенность или просто гетерогенность связана со скрытыми вмешивающимися факторами.
В данной публикации мы глубже затронем методы выявления скрытой гетерогенности и оценки публикационных смещений, а также приведем способы расчета наиболее частых статистик, используемых для оценки размера эффекта в мета-анализе.
АНАЛИЗ ПОДГРУПП
К методам, позволяющим выявить скрытые вмешивающиеся факторы (конфаундеры или модераторы), относят анализ подгрупп и метарегрессионный анализ. Оба метода имеют свои преимущества и недостатки.
При реализации анализа подгрупп исследуемую выборку разделяют по заданному признаку на подгруппы для проведения между ними сравнительного анализа. Так, при оценке распространенности сердечно-сосудистых заболеваний модераторами являются пол и возраст пациентов. В связи с этим для корректной оценки необходимо рассчитывать распространенность сердечно-сосудистых заболеваний отдельно в подгруппах пациентов, выделенных по полу и возрасту (например, по десятилетиям жизни). Кроме того, анализ подгрупп может использоваться для ответа на специфичные исследовательские вопросы о конкретных группах интереса. Например, в исследовании, в котором принимали участие пациенты с сахарным диабетом, было обнаружено положительное влияние экспериментального воздействия на уровень протеинурии. В связи с этим при апостериорном анализе исследователи выделили подгруппу пациентов с хронической болезнью почек для более детального изучения влияния экспериментального препарата на функцию почек. Однако подобное разделение на подгруппы возможно провести только при наличии исходных данных пациентов. В опубликованных исследованиях клинические данные, как правило, представлены в обобщенном виде, что затрудняет применение анализа подгрупп в явном виде при проведении мета-анализа.
Тем не менее, имея обобщенные результаты опубликованных клинических исследований, применить метод анализа подгрупп в мета-анализе для получения усредненной оценки размера эффекта можно следующим образом. На первом этапе необходимо оценить внутригрупповой размер эффекта, на втором этапе – межгрупповой размер эффекта [2].
Внутригрупповой анализ
Предположим, что нам необходимо оценить различия в размере эффекта между двумя экспериментальными препаратами (препарат А и препарат В). Мы можем разделить отобранные для мета-анализа клинические исследования на необходимое количество групп (в нашем случае две) в зависимости от типа используемого медицинского препарата. Затем мы рассчитаем средний размер эффекта в каждой подгруппе, используя модели с фиксированными или случайными эффектами. Методику применения вышеуказанных моделей и расчета взвешенного размера эффекта по нескольким исследованиям мы подробно обсуждали в нашей предыдущей публикации [1].
Модель с фиксированными эффектами корректно применять, если мы считаем, что исследования в подгруппах похожи друг на друга по дизайну, методологии и другим характеристикам. Примером корректного использования модели с фиксированными эффектами может быть следующая гипотетическая ситуация. Фармакологическая компания провела несколько сходных исследований по изучению экспериментального препарата А в сравнении с плацебо и также несколько сходных исследований по изучению экспериментального препарата B в сравнении с плацебо. Наша цель заключается в обобщении размера эффекта отдельно для препарата А и препарата B. В реальной жизни подобная ситуация редка. Если мы имеем несколько клинических исследований, выполненных разными коллективами авторов, в разных странах, по разным протоколам и клиническим рекомендациям, то мы ожидаем наличие различий между этими исследованиями в истинном размере эффекта. В таком случае корректно применять модель со случайными эффектами, позволяющую учесть влияние множества случайных факторов на истинный размер эффекта.
Межгрупповой анализ
На втором этапе анализа подгрупп необходимо провести сравнение полученных средних размеров эффектов между группами и рассчитать стандартную ошибку для разницы средних [2]. Разница средних между группами рассчитывается так же, как и разница средних для исследований, включенных в мета-анализ (формула 5).
Для модели с фиксированными эффектами дисперсия для разницы средних размеров эффектов оценивается как сумма дисперсий каждой группы:
VDiff = VA + VB, (1)
где VDiff – дисперсия разницы средних;
VA – дисперсия для группы А;
VB – дисперсия для группы B.
Для модели со случайными эффектами при расчете дисперсии для разницы средних размеров эффектов дополнительно учитывается межгрупповая дисперсия:
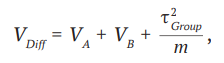 (2)
(2)
где τ2Group – межгрупповая дисперсия;
m – количество подгрупп.
Нельзя оставить без внимания слабые стороны анализа подгрупп. Так, разделение выборки на подгруппы нарушает принцип рандомизации, потому повышает вероятность получения как ложноположительных, так и ложноотрицательных результатов. Выводы, полученные при анализе подгрупп, не следует трактовать однозначно. Поскольку разделение на подгруппы проводится, как правило, после завершения клинических испытаний, существует риск выявления случайных, при этом статистически значимых различий, в связи с чем результаты анализа подгрупп необходимо подвергать критическому обсуждению. Более того, необходимо отметить, что даже при выявлении статистически значимых различий при количественной оценке эффекта раздельно в подгруппах мы не можем полностью объяснить имеющуюся гетерогенность различиями по признаку, по которому мы разделили выборку на подгруппы. Это связано с тем, что подгруппы с высокой вероятностью будут отличаться не только по «разделяющему», но и по другим признакам. Таким образом, между выделенными нами подгруппами всегда будет присутствовать неучтенная гетерогенность, связанная с наличием скрытых модераторов.
МЕТАРЕГРЕССИОННЫЙ АНАЛИЗ
Метарегрессия – это углубленный анализ подгрупп, позволяющий одновременно учитывать различные скрытые модераторы, как числовые, так и категориальные. Метарегрессионный анализ подразумевает построение регрессионной модели, где в качестве переменной исхода выступает оценка размера эффекта, а в качестве параметров модели – характеристики включенных в анализ исследований – модераторы, как качественные, так и количественные (3). Коэффициенты метарегрессионной модели показывают величину и направление влияния каждого модератора на размер эффекта в исследовании.
θk = αXk + ϵk , (3)
где θk – наблюдаемый эффект исследования k;
Xk – вектор, содержащий модераторы исследования k;
α – вектор коэффициентов регрессионной модели;
ϵk – отклонение наблюдаемого в исследовании эффекта от истинного эффекта.
Однако даже при применении метарегрессионного анализа присутствует остаточная гетерогенность, так как часть модераторов может быть не учтенной. Поэтому введено понятие метарегрессии со случайными эффектами, где учитывается случайная гетерогенность по аналогии с мета-анализом со случайными эффектами [3]. Реализация метарегрессионного анализа доступна с помощью пакета metafor1 языка программирования R.
Результаты метарегрессионного анализа можно представить графически в виде пузырьковой диаграммы (рис. 1). Данные для построения графика по эффективности вакцины против туберкулеза находятся в открытом доступе и сопровождают библиотеку metafor языка программирования R. На графике представлена однофакторная модель зависимости размера эффекта (относительный риск) от модератора (градус широты) со случайными эффектами. Каждая точка на графике обозначает размер эффекта в конкретном исследовании. Размер каждой точки пропорционален значимости исследования в оценке общего размера эффекта. Прямая толстая линия – линия регрессии, дугообразные линии с закрашенной серой областью представляют 95% доверительный интервал для регрессионной оценки. Исследование, расположенное на графике ближе к экватору (точка 8), имело относительный риск, равный 1, что означало отсутствие эффекта вакцины в данном исследовании. По мере отдаления от экватора прослеживается увеличение размера эффекта в исследованиях. В исследованиях, расположенных на графике дальше от экватора (точки 4, 2), ожидаемый размер эффекта был наибольшим, при этом относительный риск менее 1 можно интерпретировать как более высокую эффективность вакцинации в этих исследованиях. В исследованиях 12 и 13 применение вакцины оказалось неэффективным, однако нужно учесть, что в этих исследованиях было много методологических неточностей, поэтому на графике они оказались в виде выбросов.
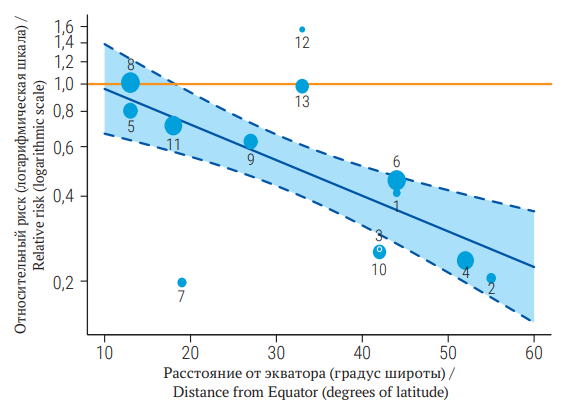
РИС. 1. Зависимость отношения рисков от градуса широты, полученная при метарегрессионном анализе 13 клинических исследований, адаптировано из C. Berkey и соавт. [3].
FIG. 1. Risk ratio versus latitude from a meta-regression based on 13 clinical studies, adapted from C. Berkey et al. [3]
Проведение метарегрессионного анализа требует соблюдения определенных условий.
- Количество исследований. В общем случае применение метарегрессии возможно, если в мета-анализ включено, как минимум, 10 исследований. Однако при большом количестве модераторов и их неравномерном распределении между включенными исследованиями для получения значимых результатов требуется увеличение выборки.
- Предварительный выбор потенциальных модераторов. Составление протокола исследования с перечислением модераторов, которые планируется включить в метарегрессионный анализ, позволит как ограничить количество анализируемых подгрупп, так и избежать ложных результатов в связи со случайно обнаруженным в ходе исследования модератором. Конечно, при выявлении в процессе проведения анализа результатов новых сильных модераторов исследователь может провести дополнительные сравнения, однако такой анализ корректно обозначать как апостериорный (post hoc).
- Ограничение количества модераторов. С увеличением количества анализируемых вмешивающихся факторов растет вероятность получения ложных результатов, поскольку при множественных сравнениях проводится коррекция статистически значимого уровня, достигнуть которого становится сложнее.
- Рациональный выбор модераторов. Для получения интерпретируемых результатов выбор анализируемых модераторов должен быть научно и клинически обоснован. Кроме того, нужно четко различать прогностические факторы, которые непосредственно влияют на исход заболевания, и модераторы, которые влияют на само вмешательство и модифицируют эффект этого вмешательства на исход. Для анализа подгрупп и построения метарегрессионной модели некорректно использовать прогностические факторы. Например, при оценке смертности от онкологических заболеваний курение может выступать в качестве прогностического фактора, так как непосредственно влияет на смертность, поэтому этот фактор корректнее включать в модель, прогнозирующую исход заболевания. А возраст, условия проведения эксперимента, доза исследуемого препарата и дизайн исследования являются модераторами, которые можно включать в качестве параметров в метарегрессионную модель, оценивающую влияние модераторов на размер эффекта. Необходимо отметить, что отнесение фактора к прогностическому или к модератору зависит от целей конкретного исследования.
- Влияние модератора может быть выявлено не всегда. Например, в несколько клинических исследований включали участников от 18 до 60 лет. В каждом отдельном исследовании может присутствовать взаимосвязь между возрастом и наблюдаемым эффектом. Однако если средний возраст между разными клиническими исследованиями сопоставим, то на уровне метарегрессионного анализа возраст окажется незначимым модератором. Подобный феномен получил название систематической ошибки агрегирования или экологического смещения.
- Мультиколлинеарность модераторов. Мультиколлинеарными или взаимосвязанными считают модераторы, эффект которых на вмешательство нельзя разделить. Например, в исследованиях, где применяли более высокие дозы глюкокортикостероидов, участвовали пациенты с более тяжелым течением заболевания. В такой ситуации невозможно однозначно определить, что оказало больший эффект на результат лечения (доза препарата или тяжесть течения заболевания). Проверить модераторы на мультиколлинеарность можно с помощью корреляции. Выявление высокой корреляции свидетельствует о взаимосвязи модераторов, в таком случае для метарегрессионного анализа нужно выбрать лишь один из них.
СМЕЩЕНИЯ В ПУБЛИКАЦИЯХ
Мы выяснили, как выявить и количественно оценить влияние модераторов на размер эффекта в исследовании. В нашей предыдущей статье мы узнали, как визуально оценить риск наличия публикационных смещений в исследовании и как в общем случае рассчитать веса исследований в усредненной оценке размера эффекта [1]. Поиск и оценка смещений в публикациях играют важную роль, поскольку смещения влияют на корректность выводов, полученных при проведении мета-анализа. Далее мы подробнее остановимся на том, как математически оценить публикационные смещения и учесть их оценку в общей усредненной оценке размера эффекта при проведении мета-анализа.
Существуют два основных подхода к оценке публикационных смещений: аналитический и графический.
Аналитический подход
Аналитический подход представляет построение аналитической модели с целью отбора публикаций для включения в мета-анализ. Отборочные модели основаны на учете весов каждого исследования. В общем виде формулу для модели отбора можно представить следующим образом (4) [4–6]:
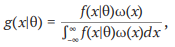 (4)
(4)
где g(x|θ) – функция отбора исследования;
x – наблюдаемый в исследовании размер эффекта;
θ – истинный средний размер эффекта;
f(x|θ) – функция плотности вероятности х;
ω(x) – функция, задающая вес исследования;
интегральное выражение – вероятность включения исследования в мета-анализ.
Функции, задающие вес исследования, подробно обобщены в обзоре A. Sutton и соавт. [6]. Интерпретировать функцию весов можно следующим образом: чем выше значимость результатов исследования, тем вероятнее оно будет включено в мета-анализ. Для построения подобных аналитических моделей необходимо включение в мета-анализ не менее 10 исследований. Недостатком аналитического подхода является трудоемкость расчетов, а также то, что выбор функции весов основан на аналитических допущениях, поэтому интерпретация результата отборочной модели может представлять трудности.
Графический подход
Более применимым в практике методом оценки публикационных смещений представляется графический подход, реализация которого доступна при помощи готовых статистических пакетов, например библиотеки metafor языка программирования R. Графический подход для анализа публикационных смещений основан на оценке воронкообразных диаграмм (funnel plots), демонстрирующих зависимость размера эффекта от точности исследования. Размер эффекта и точность результатов исследования могут быть выражены различными статистиками в зависимости от поставленной цели. Наиболее часто оценка точности исследования в мета-анализе представлена стандартной ошибкой или обратной стандартной ошибкой (precision) в случае включения в мета-анализ одновременно как крупных, так и небольших исследований [7]. О вариантах оценки размера эффекта мы поговорим в следующем разделе. Воронкообразную диаграмму можно оценивать как визуально, так и статистическими методами. Статистические методы основаны на математической оценке асимметрии воронкообразных диаграмм и включают регрессию Эггера [8], ранговую корреляцию Бегга [9] и их различные модификации [10–12].
Симметричность воронкообразной диаграммы свидетельствует об отсутствии публикационных смещений (рис. 2). Для демонстрации представлены сгенерированные из нормального распределения данные, имитирующие результаты 20 исследований. Каждая точка на графике соответствует отдельному клиническому исследованию. На воронкообразных диаграммах по оси Х принято указывать статистику, оценивающую размер эффекта (в данном случае корреляция), по оси У – статистику, оценивающую точность результатов исследования [7]. В зависимости от выбранной статистики для оценки точности исследования воронкообразные диаграммы могут иметь различную форму (рис. 2). Средняя линия обозначает истинный средний размер эффекта, а боковые закрашенные области – доверительные интервалы для размера эффекта.
При наличии публикационных смещений исследования будут размещены несимметрично относительно истинного среднего размера эффекта (рис. 3). На графике представлены данные, находящиеся в открытом доступе, по эффективности вакцины против туберкулеза, которые мы обсуждали ранее. В данном случае в качестве статистики, оценивающей размер эффекта, использовали отношение рисков. Чем меньше стандартная ошибка и дисперсия у размера эффекта, тем выше точность исследования и тем ближе точка исследования расположена к верхушке диаграммы, и, наоборот.
Еще один метод оценки устойчивости результатов мета-анализа – анализ чувствительности, основанный на поочередном исключении исследований из мета-анализа, и его графическое представление мы обсуждали в нашей предыдущей статье [1].
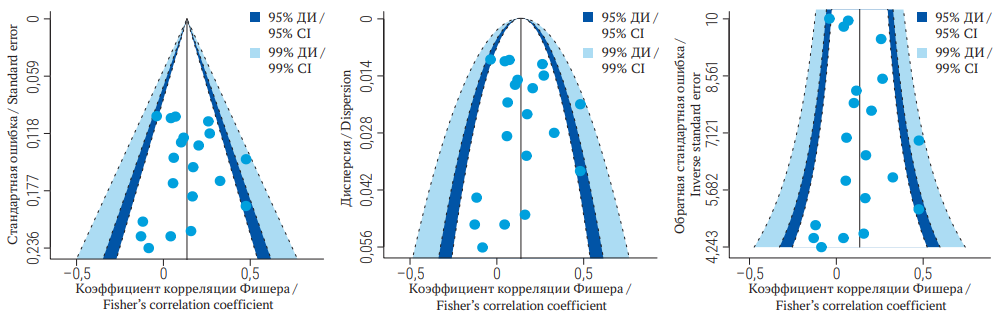
РИС. 2. Воронкообразная диаграмма, полученная при мета-анализе 20 сгенерированных исследований.
Примечание: ДИ – доверительный интервал.
FIG. 2. Funnel plots for a meta-analysis of 20 randomly generated trials.
Note: CI – confidence interval.
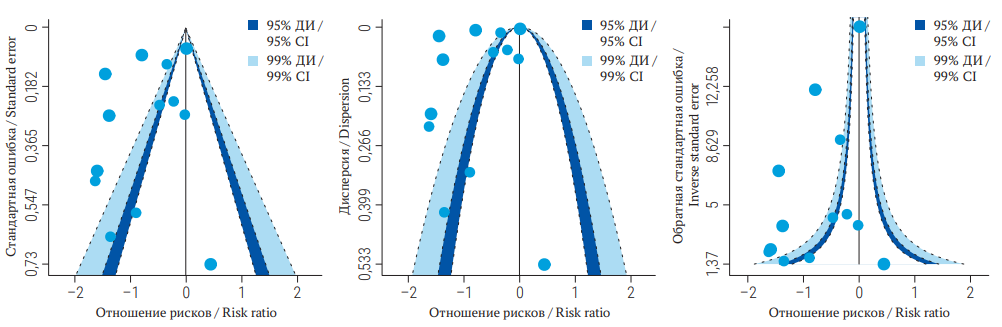
РИС. 3. Воронкообразная диаграмма, полученная при мета-анализе 13 клинических исследований.
Примечание: ДИ – доверительный интервал.
FIG. 3. Funnel plots for a meta-analysis of 13 clinical trials.
Note: CI – confidence interval.
ОЦЕНКА РАЗМЕРА ЭФФЕКТА В МЕТА-АНАЛИЗЕ
До сих пор мы использовали понятие размер эффекта, истинную оценку которого мы планируем получить при проведении мета-анализа. Размер эффекта может быть представлен различными статистиками в зависимости от единиц измерения, в которых выражен исход в публикациях. Далее мы обсудим наиболее часто употребляемые статистики для оценки размера эффекта и их формальное представление.
Разница средних (mean difference) и стандартизированная разница средних (standardized mean difference) – наиболее часто используемые статистики в мета-анализе для оценки размера эффекта результатов исследования, выраженных непрерывными числовыми значениями.
Разница средних (5) с дисперсией (6) оценивает абсолютную разницу между средними величинами в двух группах [13]; иными словами, оценивает среднюю величину, на которую экспериментальное вмешательство изменяет исход в сравнении с контрольным вмешательством. Применение разницы средних в мета-анализе возможно, если величины исходов в исследованиях представлены в одинаковых шкалах и единицах измерения.
μi = μiT – μiC, (5)
где μi – разница средних i-го исследования;
μiT – среднее значение эффекта в i-й экспериментальной группе;
μiС – среднее значение эффекта в i-й контрольной группе.
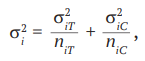 (6)
(6)
где σi2 – дисперсия разницы средних i-го исследования;
σi2T – дисперсия эффекта в i-й экспериментальной группе;
σi2C – дисперсия эффекта в i-й контрольной группе;
niT – размер экспериментальной выборки в i-м исследовании;
niC – размер контрольной выборки в i-м исследовании.
Стандартизированную разницу средних (7) с дисперсией (8) необходимо использовать, когда переменные одного и того же исхода в разных исследованиях, включенных в мета-анализ, выражены в различных шкалах и/или единицах измерения [13].
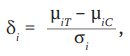 (7)
(7)
где δi – стандартизированная разница средних i-го исследования;
μiT – среднее значение эффекта в i-й экспериментальной группе;
μiС – среднее значение эффекта в i-й контрольной группе;
σi – стандартное отклонение стандартизированной разницы средних i-го исследования.
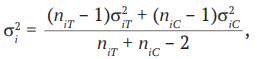 (8)
(8)
где σi2 – дисперсия стандартизированной разницы средних i-го исследования;
σi2T – дисперсия эффекта в i-й экспериментальной группе;
σi2C – дисперсия эффекта в i-й контрольной группе;
niT – размер экспериментальной выборки в i-м исследовании;
niC – размер контрольной выборки в i-м исследовании.
Преимуществом использования стандартизированного показателя является возможность сравнения результатов между различными исследованиями, чего не позволяет показатель (абсолютной) разницы средних. Стандартизированная разница средних может принимать значения от 0 до 1, при этом значение 0,2 интерпретируется как малый; 0,5 – средний и 0,8 – большой размер эффекта [14]. Однако показатели разницы средних и стандартизированной разницы средних не учитывают разнонаправленные шкалы. Например, в мета-анализ включены исследования, где оценивают выраженность депрессии по 10-бальной шкале, при этом в одном исследовании больший балл по шкале свидетельствует о более тяжелом течении заболевания, а в другом, наоборот, о более легком течении депрессии. В таком случае перед расчетом разницы средних или стандартизированной разницы средних необходимо вручную привести шкалы к одному направлению (например, домножив одну из шкал на минус 1).
Отношение средних (ratio of means) – еще один подход к оценке размера эффекта в мета-анализе для исходов, выраженных непрерывными числовыми значениями [15], показывающий, во сколько раз экспериментальное вмешательство изменяет исход в сравнении с контрольным вмешательством. Преимуществом данной статистики является независимость оценки размера эффекта от различных шкал и/или единиц измерения переменных исходов в исследованиях, включенных в мета-анализ. Однако расчет отношения средних корректен только в случаях, когда переменная исхода может выражаться положительными, но не отрицательными единицами измерения.
Другими мерами оценки размера эффекта количественных переменных может быть стандартизированная разница в терминах минимально значимой разницы, разница в процентах от исходного уровня и другие. Для оценки размера эффекта категориальных данных используют отношение пропорциональных шансов (proportional odds ratios), временных рядов – отношение рисков (hazard ratio), переменных счета – отношение частот (rate ratio).
ЗАКЛЮЧЕНИЕ
В настоящей статье мы обсудили методы количественной оценки гетерогенности, их преимущества, недостатки и необходимые условия, а также математическую реализацию и интерпретацию графического представления метарегрессионного анализа. Кроме того, мы узнали, как проводить оценку публикационных смещений аналитическими и графическими методами и как учитывать публикационные смещения в оценке общего размера эффекта при проведении мета-анализа. Также мы остановились на статистиках, используемых для оценки размера эффекта, и привели пример расчета наиболее часто используемых статистик и их стандартных отклонений.
Конфликт интересов. М.Ю. Бровко – член редакционной коллегии, М.Ю. Надинская – научный редактор журнала: оба не принимали участия в редакционном рассмотрении и принятии решений по данной статье.
Финансирование. Статья подготовлена при поддержке программы стратегического академического лидерства «Приоритет-2030» ФГАОУ ВО «Первый МГМУ им. И.М. Сеченова» Минздрава России (Сеченовский Университет).
Conflict of interests. Mikhail Yu. Brovko is an editorial board member and Maria Yu. Nadinskaia is a scientific editor of the journal: both had no role in the editorial review and decision making for this article.
Financial support. This article was supported by the Academic leadership program Priority 2030 proposed by Sechenov First Moscow State Medical University (Sechenov University).
1 https://metafor-project.org/doku.php/metafor (access date 04.06.2024).
Список литературы
1. Suvorov A.Y., Latushkina I.V., Gulyaeva K.А., et al. Basic aspects of meta-analysis. Part 1. Sechenov Medical Journal. 2023; 14(1): 4–14. https://doi.org/10.47093/2218-7332.2023.14.1.4-14
2. Borenstein M., Higgins J.P.T. Meta-Analysis and Subgroups. Prev Sci. 2013 Apr; 14(2): 134–143. https://doi.org/10.1007/s11121013-0377-7. PMID: 23479191
3. Berkey C.S., Hoaglin D.C., Mosteller F., Colditz G.A. A randomeffects regression model for meta-analysis. Stat Med. 1995 Feb 28; 14(4): 395–411. https://doi.org/10.1002/sim.4780140406. PMID: 7746979
4. Hedges L.V. Modeling publication selection effects in metaanalysis. J Phys A Math Theor. 1992; 7(2): 246–255. https://doi.org/10.1088/1751-8113/44/8/085201
5. Dear K.B.G., Begg C.B. An approach for assessing publication bias prior to performing a meta-analysis. Stat Sci. 1992; 7(2): 237–245. https://doi.org/10.1214/ss/1177011363
6. Sutton A.J., Song F., Gilbody S.M., Abrams K.R. Modelling publication bias in meta-analysis: a review. Stat Methods Med Res. 2000 Oct; 9(5): 421–445. https://doi.org/10.1177/096228020000900503. PMID: 11191259
7. Sterne J.A.C., Egger M. Funnel plots for detecting bias in meta-analysis: guidelines on choice of axis. J Clin Epidemiol. 2001 Oct; 54(10): 1046–1055. https://doi.org/10.1016/S08954356(01)00377-8. PMID: 11576817
8. Egger M., Smith G.D., Schneider M., Minder C. Bias in metaanalysis detected by a simple, graphical test. BMJ. 1997 Sep 13; 315(7109): 629–634. https://doi.org/10.1136/bmj.315.7109.629. PMID: 9310563; PMCID: PMC2127453
9. Begg C.B., Mazumdar M. Operating characteristics of a rank correlation test for publication bias. Biometrics. 1994 Dec; 50(4): 1088–1101. https://doi.org/10.2307/2533446. PMID: 7786990
10. Harbord R.M., Egger M., Sterne J.A.C. A modifi ed test for smallstudy effects in meta-analyses of controlled trials with binary endpoints. Stat Med. 2006 Oct 30; 25(20): 3443–3457. https://doi.org/10.1002/sim.2380. PMID: 16345038
11. Macaskill P., Walter S.D., Irwig L. A comparison of methods to detect publication bias in meta-analysis. Stat Med. 2001 Feb 28; 20(4): 641–654. https://doi.org/10.1002/sim.698. PMID: 11223905.
12. Lin L., Chu H. Quantifying publication bias in meta-analysis. Biometrics. 2018 Sep; 74(3): 785–794. https://doi.org/10.1111/biom.12817. Epub 2017 Nov 15. PMID: 29141096; PMCID: PMC5953768
13. Bakbergenuly I., Hoaglin D.C., Kulinskaya E. Estimation in meta-analyses of mean difference and standardized mean difference. Stat Med. 2020 Jan 30; 39(2): 171–191. https://doi.org/10.1002/sim.8422. Epub 2019 Nov 11. PMID: 31709582; PMCID: PMC6916299
14. Cohen J. Statistical Power Analysis for the Behavioral Sciences. Second Edition. New Jersey: Lawrence Erlbaum Associates; 1988. 579 p. ISBN 0-8058-0283-5
15. Friedrich J.O., Adhikari N.K.J., Beyene J. The ratio of means method as an alternative to mean differences for analyzing continuous outcome variables in meta-analysis: A simulation study. BMC Med Res Methodol. 2008; 8(1): 32. https://doi.org/10.1186/1471-2288-8-32
Об авторах
Е. А. ТаоРоссия
Тао Екатерина Александровна, канд. мед. наук, ассистент кафедры внутренних, профессиональных болезней и ревматологии
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119048
М. Ю. Надинская
Россия
Надинская Мария Юрьевна, канд. мед. наук, доцент кафедры пропедевтики внутренних болезней, гастроэнтерологии и гепатологии
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119048
А. Ю. Суворов
Россия
Суворов Александр Юрьевич, канд. мед. наук, главный статистик отдела исследовательских сервисов Управления по научному развитию и клиническим исследованиям
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119048
Н. М. Буланов
Россия
Буланов Николай Михайлович, канд. мед. наук, доцент кафедры внутренних, профессиональных болезней и ревматологии
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119048
В. И. Шоломова
Россия
Шоломова Виктория Игоревна, канд. мед. наук, доцент кафедры внутренних, профессиональных болезней и ревматологии
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119048
П. П. Потапов
Россия
Потапов Павел Петрович, ассистент кафедры внутренних, профессиональных болезней и ревматологии
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119048
М. С. Тараткин
Россия
Тараткин Марк Сергеевич, начальник отдела развития молодежной науки Управления по научному развитию и клиническим исследованиям
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119048
М. Ю. Бровко
Россия
Бровко Михаил Юрьевич, д-р. мед. наук, профессор кафедры внутренних, профессиональных болезней и ревматологии; проректор по международной деятельности
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119048