Перейти к:
Применение диаграмм Венна и теории вероятностей в клинических исследованиях
https://doi.org/10.47093/2218-7332.2020.11.4.5-14
Аннотация
В настоящее время статистика играет ключевую роль при проведении медицинских исследований, объектом ее изучения являются накопление и обобщение данных, а также интерпретация взаимосвязей между экспериментальными данными. Данная статья открывает вводный цикл, посвященный проблемам биомедицинской статистики, и знакомит читателей с диаграммами Венна, а также с базовыми концепциями теории вероятностей и теории множеств, понимание которых необходимо для освоения принципов описательной статистики и статистики вывода. В статье представлено применение диаграмм Венна в современных клинических исследованиях, а также определены пространство элементарных событий, базовые операции с множествами (объединение, пересечение) и их применение в контексте классической теории вероятностей. Все примеры проиллюстрированы диаграммами Венна.
Статистика — это наука, объектом изучения которой являются сбор, обобщение, представление и интерпретация данных для оценки силы ассоциаций и проверки гипотез [1]. В настоящее время статистические методы играют ключевую роль в медицинских и биологических исследованиях. Поэтому понимание и применение базовых подходов к анализу данных являются необходимыми навыками для всех врачей и исследователей. Однако большинство специалистов в области здравоохранения в России не имеют практически никакой математической подготовки и обладают крайне ограниченным пониманием статистики, что зачастую приводит к неверной и некритичной интерпретации публикуемых медицинских данных, а также неспособности организовать и провести собственные исследования и проанализировать их результаты должным образом. В связи с этим мы решили опубликовать цикл статей, составляющих введение в курс биомедицинской статистики.
Этот курс изначально был разработан для обучающихся по программам магистратуры и PhD Университетского колледжа Лондона, а позднее адаптирован для студентов и обучающихся по программам постдипломного образования Сеченовского Университета. Основная цель курса — практическое применение полученных знаний, поэтому основное внимание в статьях будет уделено наиболее важным математическим концепциям
и статистическим методам, которые необходимы для критического понимания современных клинических исследований, а также подготовки публикаций, соответствующих требованиям высокорейтинговых медицинских журналов.
Мы настоятельно рекомендуем читателям научиться самостоятельно представлять полученные данные в адекватной форме, использовать базовые статистические тесты и интерпретировать полученные результаты без помощи профессионального статистика. Однако мы также включили в этот курс описание более сложных статистических методов, таких как алгоритмы машинного обучения, для того чтобы познакомить читателей с возможными областями их применения. Еще одной целью этого курса является обеспечение эффективного сотрудничества между врачами и статистиками для разработки рационального дизайна клинических исследований, формулирования реалистичных целей, выбора оптимальных подходов и адекватной интерпретации результатов исследования. Все методы, обсуждаемые в статьях, могут быть использованы в любых статистических программах, как коммерческих (SPSS, Stata, SAS, MatLab и др.), так и бесплатных (R).
Материал подготовлен с учетом отсутствия математической подготовки у большинства читателей. Однако в курсе будут в упрощенном виде представлены некоторые математические концепции и формулы, поскольку, с точки зрения авторов, это наиболее подходящий способ представления идей, лежащих в основе методов статистического анализа данных. Курс представлен на русском и английском языках, чтобы познакомить читателей с наиболее часто используемыми в научных публикациях терминами.
Первая статья посвящена основам теории множеств и теории вероятностей и проиллюстрирована примерами с использованием диаграмм Венна.
ДИАГРАММЫ ВЕННА
Диаграммы Венна, также известные как диаграммы множеств, часто используют для иллюстрации логических взаимосвязей между двумя и более наборами данных в публикациях, освещающих результаты клинических и эпидемиологических исследований. Диаграмма Венна состоит из частично перекрывающих друг друга окружностей или других замкнутых кривых, демонстрирующих взаимосвязь и группировку множеств данных, которые могут быть общими для различных выборок или не пересекаться. Диаграммы Венна впервые были представлены Джоном Венном, преподавателем гуманитарных наук в Caius College Кембриджского университета, в статье под названием «О схематическом и механическом представлении суждений и рассуждений», опубликованной в 1880 г. [2]. Примечательно, что если проследить историю использования методов визуализации в области формальной логики, можно обнаружить, что диаграммы, ассоциируемые с именем Венна, по всей видимости, впервые были созданы существенно раньше [3]. Чтобы больше узнать об истории диаграмм Венна, читатели могут обратиться к другим публикациям [4].
По мере накопления знаний о сложности физиологических и молекулярных процессов все большее значение приобретает анализ мультиомики и больших данных (Big Data). Возрастает потребность разработки новых методов одновременной оценки большого числа наборов данных [5], в связи с чем даже классические методы визуализации, такие как диаграммы Венна, претерпели дальнейшее развитие. В настоящее время диаграммы Венна широко используют в клинических исследованиях, в частности для изучения микробиома [6] или обструктивных заболеваний легких [7], другой сферой их применения являются генетические исследования [8]. Графическое отображение взаимодействий легко воспринимается, поскольку отражает логические взаимосвязи и пересечения множеств.
В настоящее время для работы с четырьмя независимыми наборами данных доступны многочисленные онлайн-программы для построения диаграмм Венна, например генератор диаграмм Венна Pangloss1 или Venny2 . Эти программы весьма удобны в применении, однако создают лишь изображения без значимой сопутствующей информации. BioVenn [9] является примером программ, позволяющих создавать диаграммы пропорциональной площади и проводить их анализ. Программы GeneVenn3 и VennMaster4 обладают дополнительной функцией привязки генов в каждой группе к ассоциированной информации в базах данных NCBI Entrez Nucleotide и Gene Ontology, однако в них можно проводить анализ лишь двух или трех панелей генов [8][10].
Для баз данных микрочипов можно использовать специально разработанные для этих целей программы GeneSpring и SilicoCyte, в которых возможно и построение диаграмм Венна. Визуализация пересечений может создавать проблемы при работе с более чем тремя выборками из-за возможных нарушений симметрии изображений. Сам Венн в подобных случаях использовал дополнительные эллипсы, которые пересекались с основными окружностями [2]. Впоследствии A.W.F. Edwards разработал элегантный метод изображения диаграмм, включающих большее число множеств, с использованием необычных типов симметрии [11]. Далее представлен пример создания диаграмм Эдвардса — Венна, который можно с легкостью провести в свободно доступной программе VENNTURE5 [5].
Используя программу VENNTURE, создадим диаграмму Эдвардса — Венна для абстрактного примера. Давайте представим, что в городе есть шесть аптек, которые могут продавать 26 наименований препаратов, и их можно обозначить буквами английского алфавита. Однако в ассортименте каждой аптеки может быть только 20 различных препаратов в связи с ограниченным местом хранения на складе. Предположим, что препараты были случайным образом распределены между аптеками. Используя диаграммы Венна, можно проанализировать, как именно они были распределены. Этот процесс изображен на рисунке 1 для 2 (A), 3 (B), 5 (C) и 6 (D) наборов данных, представляющих ассортимент препаратов в соответствующих аптеках. На рисунке 1A видно, что в обеих аптеках есть в наличии 15 препаратов, поскольку они попадают в пересечение наборов, обозначенных красным (первая аптека) и синим (вторая аптека) цветами. А пять препаратов есть в наличии только в одной из них. Предложенный метод визуализации позволяет отобразить до 6 наборов данных. Например, из рисунка 1B понятно, что препарат «O» можно найти только в первой аптеке, в то время как 10 препаратов продаются во всех трех исследуемых аптеках. Также становится понятно, что шесть препаратов можно найти в пяти аптеках (рис. 1C), а во всех шести аптеках — только пять препаратов (рис. 1D), поскольку в пересечение всех шести множеств попали только буквы «DFGSZ».
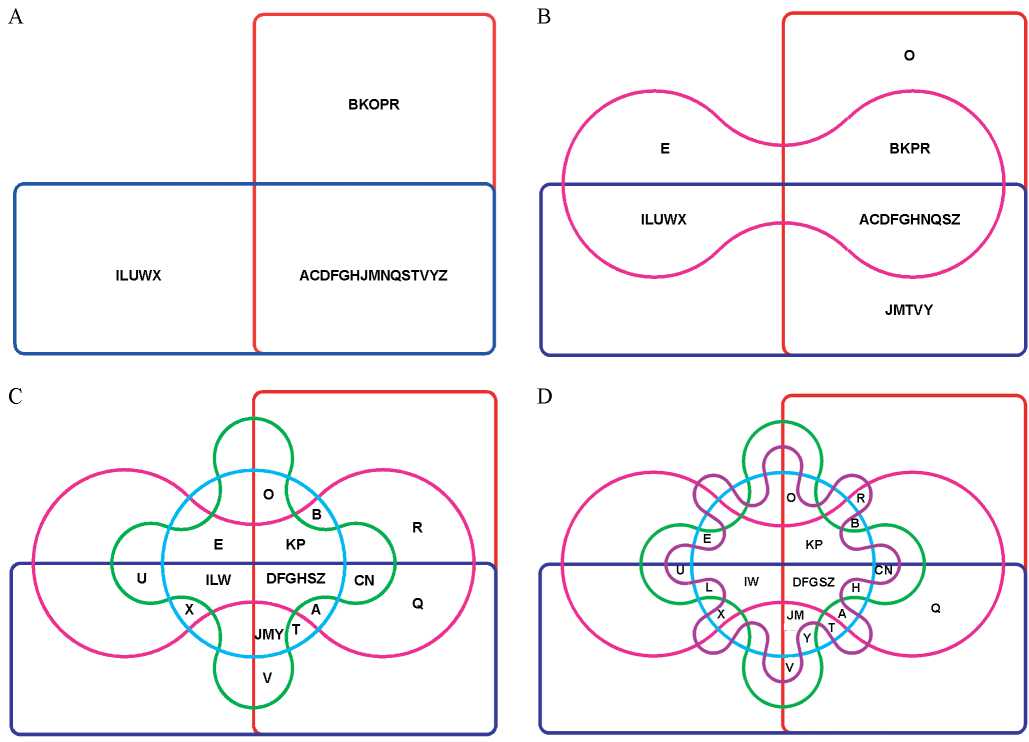
FIG. 1. Edwards—Venn diagram representing overlaps of 2 (A), 3 (B), 5 (C) and 6 (D) datasets in a symmetric way.
РИС. 1. Диаграммы Эдвардса — Венна, симметрично изображающие пересечения 2 (A), 3 (B), 5 (C) и 6 (D) наборов данных.
Примечание. Символы, которые являются общими для соответствующих наборов данных, изображены в области их пересечения.
Note. The symbols, which are common in the corresponding sets, are displayed at the intersections between these datasets.
РУКОВОДСТВО: ТЕОРИЯ МНОЖЕСТВ И ДИАГРАММЫ ВЕННА
Диаграммы Венна легче понять, если рассмотреть их связь с теорией вероятностей и теорией множеств. Вероятность — это способ выразить представление о каком-либо событии, которое произошло или может произойти. Любой процесс наблюдения событий в реальном мире можно назвать «экспериментом». Результаты эксперимента — это его исходы. В целом концепция вероятности нужна для формализации принципов получения данных в наблюдениях. Любая модель, описанная в терминах вероятности («идеальный мир» модели), может быть изучена с помощью математических свойств, позволяющих понять закономерности и предсказать некоторые события, которые могут произойти в будущем или в других условиях (например, в клинических исследованиях). Статистика, напротив, изучает частоту уже произошедших в реальных условиях событий (например, ретроспективные данные или клинические исследования), чтобы оценить вероятность наблюдаемых событий и создать или протестировать подходящую модель вероятности.
Чтобы дать математическое определение вероятности, необходимо обозначить множество S, включающее в себя все возможные результаты эксперимента. Элемент «s» множества S называют элементарным событием. Пространство элементарных событий S называют:
- дискретным, если оно состоит из конечного числа элементарных событий;
- исчислимым, если все его элементы можно сопоставить с последовательностью положительных целых чисел (1, 2, 3, 4, …);
- непрерывным, если все элементарные события составляют континуум;
- пустым или нулевым множеством, если множество не содержит элементов; подобные множества обозначают символом Ø.
Над множествами можно выполнять ряд операций, результаты которых можно отобразить с помощью диаграмм Венна (рис. 2).
Объединение (рис. 2A)

FIG. 2. Venn diagram are represented in blue: a union of events A and B, shown by two circles (A); an intersection of events A and B (B); complement to event A denoted Ā (C); and a symmetric difference of A and B (D).
РИС. 2. Диаграммы Венна, на которых синим цветом обозначено: объединение A и B, представленных двумя окружностями (A); пересечение A и B (B); событие, противоположное A, обозначаемое Ā (C); симметричная разность A и B (D).
События A и B в множестве S можно объединить, получив в результате более крупное событие. Объединение A ⋃ B возникает, когда случается одно событие или оба:
A ⋃ B = {все исходы в А или в В или в А и В вместе}
Если мы наблюдаем некое число событий Ei, равное n (где i — число от 1 до n), их объединение обозначают:
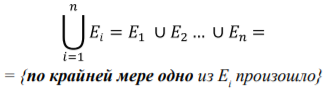
Объединение обладает следующими свойствами:
1. Объединение события A с пустым множеством равно событию A (закон тождества):
A ⋃ Ø = А
2. Объединение события A с самим собой равно событию A (закон идемпотентности/одинаковости):
A ⋃ A = А
3. Объединение события A с пространством элементарных событий равно пространству элементарных событий, или, иными словами, пространство элементарных событий доминирует над отдельным событием (закон доминирования):
A ⋃ S = S
4. Объединение событий A и B равно объединению событий B и A (коммутативный/переместительный закон):
A ⋃ B = B ⋃ А
Примеры:
1.1. Результаты подбрасывания монеты можно обозначить как A, если выпадает орел (A = {О}), и B, если выпадает решка (B = {Р}). Объединение событий A и B будет включать в себя два элемента — выпадение и орлов, и решек (A ⋃ B = {О, Р}) и фактически равно всему пространству элементарных событий для данной модели.
1.2. Если обозначить результаты броска игральной кости при выпадении 1, 3 и 4 как событие E (E = {1,3,4}) а при выпадении 1, 2 и 3 как событие F (F = {1,2,3}), объединение событий E и F будет равно 1,2,3,4 (E ⋃ F = {1,2,3,4}). Обратите внимание, что результаты 1 и 3 присутствуют в обоих событиях, но при объединении учитываются лишь однократно.
1.3. При игре в рулетку объединение всех нечетных результатов будет равно S = {0} ⋃ {1,3, …, 33}.
Пересечение (рис. 2B)
Пересечение событий A ∩ B позволяет создать новое событие, которое объединяет элементы, входящие одновременно и в A, и в B и возникающее, когда одновременно происходят события A и B.
A ∩ B = {все исходы и в А и в В}
Пересечение некоторого числа событий Ei, равного n (где i — число от 1 до n) обозначают:
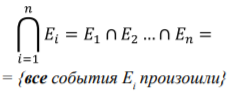
Комплементарное (противоположное) событие и симметричная разность (рис. 2C и D)
Событие, противоположное A, или событие «не A» (обозначается Ā) включает в себя все исходы, которые не входят в A (рис. 2C). Развитием идеи комплементарного события является симметричная разность, которая для множеств A и B представляет все события в A, не входящие в B, и все события в B, не входящие в A (рис. 2D):
A Δ B = (A\B) ⋃ (B\A)
РУКОВОДСТВО: РАЗБИЕНИЕ ПРОСТРАНСТВА ЭЛЕМЕНТАРНЫХ СОБЫТИЙ
Используя две базовые операции, объединение и пересечение, можно выполнить разбиение пространства элементарных событий. Если пересечение событий A и B равно нулю (A ∩ B = Ø), эти события являются взаимоисключающими (несовместными). Взаимоисключающие события не могут происходить одновременно, или, другими словами, у этих множеств нет общих элементов. События называют исчерпывающими, если они включают в себя все возможные исходы (подобно событиям A и B в примере 1.1 с монетой). Если события E1, E2,…, En взаимоисключающие и исчерпывающие, они формируют разбиение пространства элементарных событий (рис. 3).

FIG. 3. Events E1–E6 form the partition of the sample space.
РИС. 3. События E1–E6 образуют разбиение пространства элементарных событий.
Теория множеств позволяет интерпретировать различные ситуации, возникающие в реальном мире. А некоторые операции позволяют проследить взаимосвязи между терминологией теории вероятностей и теории множеств (табл. 1).
Таблица 1. Эквиваленты операций над множествами в теории вероятностей
Table 1. Summary of set operations and probability equivalents
|
Выражение |
Теория множеств |
Теория вероятностей |
|
S |
Все исходы |
Пространство элементарных событий |
|
s |
Элемент в S |
Элементарное событие, исход |
|
A |
Подмножество S |
Событие, при котором наблюдают исход A |
|
Ā, Ac |
Событие, противоположное A |
Событие, при котором исход A не происходит |
|
A ∩ B |
Пересечение |
И A, и B |
|
A ⋃ B |
Объединение |
Или A, или B, или оба |
|
A \ B |
Разность |
A, но не B |
|
A ∆ B |
Симметричная разность |
Или A, или B, но не оба |
|
A ∈ B |
Инклюзия |
Если A, то и B |
|
Ø |
Пустое множество |
Невозможное событие |
|
S |
Все множество |
Событие, которое произойдет наверняка |
РУКОВОДСТВО: ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Вероятность — мера количественной оценки возможности того, что событие произойдет. Возможны несколько интерпретаций вероятности. Первый подход — частотная оценка, которую получают путем вычисления доли случаев, в которых произошло некое событие, в долгосрочных сериях наблюдения при повторных экспериментах. Однако классическая интерпретация, предложенная российским математиком А.Н. Колмогоровым, определяет вероятность как величину, в равной степени распределенную между всеми возможными исходами. Таким образом, вероятность события — это доля от общего числа возможных исходов, в которых наступает исследуемое событие. Например, бросок монеты может привести лишь к двум возможным исходам: выпадению орла или решки, при этом вероятность каждого из этих событий равна 0,5.
Частотный подход к оценке вероятности (частотная вероятность) может быть проиллюстрирован следующим примером.
Предположим, что мы повторяем эксперимент N раз в абсолютно идентичных условиях. Событие A может произойти при каждом повторении эксперимента. Таким образом, если среди N наблюдений исход А наблюдали N(A) раз, то отношение N(A)/N стремится к вероятности этого события, поскольку N стремится к бесконечности:
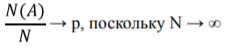
В представленном примере p — постоянная величина, отражающая вероятность наступления события A в каждом отдельно взятом эксперименте — P(A). Эта величина обладает следующими свойствами.
1. Если A равно нулю, то событие никогда не происходит и его вероятность равна нулю:
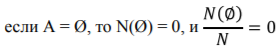
2. Если A включает в себя все возможные события, то исход наступает в каждом эксперименте, а его вероятность равна 1:
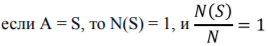
3. Если A и B — несвязанные события, то частота их объединения равна сумме частот наблюдений события A — N(A), и события B — N(B), а вероятность наблюдения их объединения будет равна сумме вероятности наступления каждого события по отдельности:

Однако этот же эксперимент можно рассмотреть и с позиции классического подхода. В таком случае эксперимент следует рассматривать как пространство элементарных событий S. Тогда для каждого события A, входящего в множество S, существует функция вероятности P(A), которая определяет вес A. Функция вероятности P(A) обладает следующими свойствами.
1. Ее величина находится в интервале от 0 до 1:
0 ≤ P(A) ≤ 1.
2. Вероятность совокупности всех возможных элементарных событий равна 1:
P (S) = 1.
3. Если события A и B не пересекаются (их пересечение равно 0), то вероятность их объединения равна сумме вероятностей наступления каждого события по отдельности:
если А ∩ В = Ø, то Р(A ⋃ B) = Р(А) + Р(В)
Используя эти аксиомы, мы можем описать функцию вероятности. Для каждой серии взаимоисключающих исходов A1, A2, … вероятность объединения будет равна сумме вероятностей каждого исхода по отдельности:

Следует помнить, что вероятности различных событий могут суммироваться. То есть, чтобы измерить вероятность множества событий, мы можем разделить его на конечное число отдельных событий, измерить вероятность каждого по отдельности и суммировать результаты.
Если событие A случается во всех наблюдениях, его вероятность равна 1 (100%):
P(A) = 1, если A случается во всех наблюдениях.
Если событие A невозможно (не случается никогда), его вероятность равна нулю:
P(A) = 0, если A невозможно.
Используя этот подход, рассмотрим несколько примеров.
Вероятность противоположного
Рассмотрим событие A, представленное белым кругом на диаграмме Венна (рис. 2C). Давайте попробуем оценить вероятность противоположного события — Ā, которое означает, что событие A не наступит — оно обозначено синим на диаграмме Венна. Используя ранее обсуждавшиеся утверждения, мы можем сделать следующие заключения.
Вероятность наступления всех возможных исходов равна 1:
Р(S) = 1P(S) = 1. (I)
Событие A и противоположное ему являются взаимоисключающими, поэтому их общая вероятность равна сумме вероятностей каждого из этих событий:
A ∩ Ā = 0 и P(A ⋃ Ā) = P(A) + P(Ā) (II)
События A и Ā являются взаимоисключающими и исчерпывающими, поэтому их объединение включает в себя все пространство элементарных событий S:
(A ⋃ Ā) = S(A ⋃ Ā) = S (III)
Обобщив заключения I–III, можно сделать вывод о том, что поскольку вероятность S равна вероятности объединения событий A и Ā, которая, в свою очередь, равна сумме вероятностей каждого из этих событий, то сумма этих вероятностей равна 1:
1 = P(S) = P(A ⋃ Ā) = P(A) + P(Ā)
Таким образом, в таких условиях вероятность развития события может быть вычислена через вероятность противоположного исхода:
P(A) = 1– P(Ā)
Вероятность объединения
Рассмотрим два возможных события, A и B в множестве S (обозначены синим на диаграмме Венна, рис. 2A). Давайте оценим вероятность наступления какого-либо из двух исходов, A или B, которая, очевидно, равна вероятности их объединения. Существенной проблемой является пересечение A и B, потому что, просто сложив вероятности A и B, мы учтем исходы в области пересечения дважды, что неверно. Чтобы оценить вероятность пересечения точно, следует принять во внимание следующее.
Объединение A и B равно объединению A с областью пересечения противоположного события Ā и события B:
A ⋃ Ā = A ⋃ (Ā ∩ B)
В свою очередь, вероятность объединения A и B равна сумме вероятностей этих двух множеств:
P(A ⋃ Ā) = P(A) ⋃ P(Ā ∩ B) (I)
С другой стороны, B можно представить в виде объединения области пересечения A и B с областью пересечения пространства вне события A (Ā) и B:
B = (A ∩ B) ⋃ (Ā ∩ B)
P(B) = P(A ∩ B) + P(Ā ∩ B) (II)
С помощью выражений I и II мы можем переписать уравнения и заменить их члены, чтобы представить вероятность объединения событий как сумму их вероятностей за вычетом вероятности их пересечения:
P(A ⋃ B) = P(A) + P(B) – P(A ∩ B)
Многократное подбрасывание монеты
Монету, вероятность выпадения как орла, так и решки у которой равна 0,5, подбрасывают несколько раз. Используя теорию вероятностей, можно доказать, что наверняка (с вероятностью, равной 1) рано или поздно орел выпадет.
Сначала можно оценить вероятность противоположного события — орел никогда не выпадет. Она равна пределу n (n стремится к бесконечности) вероятности того, что за первые n бросков орел не выпадет. Вероятность того, что будет выпадать только решка, равна ½n. Поскольку n стремится к бесконечности, значение этого уравнения стремится к нулю:
P(орел никогда не выпадет) = lim P(орел не выпадет в первые n бросков) = lim (2–n) = 0
Вероятность выпадения орла равна единице минус вероятность противоположного события (орел не выпадет), которая стремится к нулю. Таким образом, искомая вероятность равна:
P(орел выпадет) = 1 – P(орел не выпадет) = 1 – 0 = 1
Вероятность события, равная единице, означает, что орел рано или поздно выпадет.
Продолжительность жизни клеток
Последний пример демонстрирует применение теории вероятностей в биомедицинских исследованиях. Эксперимент состоит в измерении продолжительности жизни 200 клеток. Результаты представлены в таблице 2.
Таблица 2. Пример анализа продолжительности жизни клеток
Table 2. Lifetime of cells analysis example
|
Продолжительность жизни, ч |
Число клеток |
Доля |
|
<1000 |
45 |
0,225 |
|
1000–1500 |
80 |
0,400 |
|
>1500 |
75 |
0,375 |
Наша задача состоит в оценке вероятности того, что продолжительность жизни клетки составит ≤1500 ч. Сначала необходимо обозначить события: К — короткое, для исхода <1000 часов; C — среднее, для исходов в промежутке от 1000 до 1500 часов; Д — длинное, для исходов >1500 часов.
Чтобы оценить вероятность того, что продолжительность жизни составит ≤1500 часов, необходимо оценить вероятность объединения событий К и C, которая равна сумме их вероятностей, поскольку их пересечение равно нулю (взаимоисключающие события):
P(h ≤ 1500) = P(K ⋃ C) = P(K) + P(C) = 0,225 + 0,4 = 0,625
Обратите внимание, что события К, С и Д не только взаимоисключающие, но и исчерпывающие, а потому образуют разбиение пространства элементарных событий.
ЗАКЛЮЧЕНИЕ
В первой вводной статье мы представили краткий обзор области применения диаграмм Венна в современных клинических исследованиях. Следует отметить, что даже этот метод визуализации, который является классическим, продолжает активно развиваться. Мы рассмотрели базовые положения теории вероятностей, ее взаимосвязь с теорией множеств, а также применение диаграмм Венна для иллюстрации некоторых концепций. Несмотря на то что материал может показаться довольно абстрактным, он имеет критическое значение для понимания принципов статистического анализа, а диаграммы Венна нередко используют для иллюстрации в научных статьях.
ВКЛАД АВТОРОВ
Н.М. Буланов, А.А. Заикин, О.Б. Блюсс, Д.Б. Мунблит, Т.В. Назаренко и М.Ю. Надинская участвовали в написании текста рукописи. О.Б. Блюсс, Д.Б. Мунблит и Т.В. Назаренко выполняли поиск и анализ литературы по теме обзора. А.А. Заикин и Д.В. Бутнару разработали общую концепцию статьи и осуществляли руководство ее написанием. Все авторы участвовали в обсуждении и редактировании работы. Все авторы утвердили окончательную версию публикации.
AUTHOR CONTRIBUTIONS
Nikolay М. Bulanov, Alexey A. Zaikin, Oleg B. Blyuss, Daniil B. Munblit, Tatiana V. Nazarenko and Maria Yu. Nadinskaia, participated in writing the text of the manuscript. Oleg B. Blyuss, Daniil B. Munblit and Tatiana V. Nazarenko searched and analyzed the literature on the review topic. Alexey A. Zaikin and Denis V. Butnaru developed the general concept of the article and supervised its writing. All authors participated in the discussion and editing of the work. All authors approved the final version of the publication.
Конфликт интересов. Авторы заявляют об отсутствии конфликта интересов.
Финансирование. Исследование не имело спонсорской поддержки (собственные ресурсы).
Conflict of interests. The authors declare that there is no conflict of interests.
Financial support. The study was not sponsored (own resources).
1. http://www.pangloss.com/seidel/Protocols/venn.cgi
2. https://bioinfogp.cnb.csic.es/tools/venny/
3. http://genevenn.sourceforge.net/
4. https://sysbio.uni-ulm.de/?Software:VennMaster
5. https://www.nia.nih.gov/research/resource/vennture
Список литературы
1. Kirkwood B.R., Sterne J.A.C. Essential Medical Statistics (2nd ed.), Wiley-Blackwell, 2003. 512 p.
2. Venn J. On the diagrammatic and mechanical representation of propositions and reasonings. The London, Edinburgh, and Dublin philosophical magazine and journal of science, 1880; 10(59): 1–18. https://doi.org/10.1080/14786448008626877
3. Bultena B., Ruskey F. Venn diagrams with few vertices. Electronic Journal of Combinatorics. 1998; 5: R44: 1–21. https://doi.org/10.37236/1382
4. Baron M. E. A note on the historical development of logic diagrams: Leibniz, Euler and Venn. The Mathematical Gazette. 1969; 53(384): 113–125. https://doi.org/10.2307/3614533
5. Martin B., Chadwick W., Yi T., et al. VENNTURE — a novel Venn diagram investigational tool for multiple pharmacological dataset analysis. PLoS One. 2012; 7(5): e36911. https://doi.org/10.1371/journal.pone.0036911 Erratum in: PLoS One. 2012; 7(5): https://doi.org/10.1371/annotation/27f1021c-b6f2-4b90-98bc-fcacd2679185 PMID: 22606307
6. Shade A., Handelsman J. Beyond the Venn diagram: the hunt for a core microbiome. Environ Microbiol. 2012 Jan; 14(1): 4–12. https://doi.org/10.1111/j.1462-2920.2011.02585.x PMID: 22004523.
7. Soriano J.B., Davis K.J., Coleman B., et al. The proportional Venn diagram of obstructive lung disease: two approximations from the United States and the United Kingdom. Chest. 2003 Aug; 124(2):474–81. https://doi.org/10.1378/chest.124.2.474 PMID: 12907531
8. Pirooznia M., Nagarajan V., Deng Y. GeneVenn — A web application for comparing gene lists using Venn diagrams. Bioinformation. 2007 Apr 10; 1(10): 420–2. https://doi.org/10.6026/97320630001420 PMID: 17597932
9. Hulsen T., de Vlieg J., Alkema W. BioVenn — a web application for the comparison and visualization of biological lists using area-proportional Venn diagrams. BMC Genomics. 2008 Oct 16; 9: 488. https://doi.org/10.1186/1471-2164-9-488 PMID: 18925949
10. Kestler H.A., Müller A., Kraus J.M., et al. VennMaster: area-proportional Euler diagrams for functional GO analysis of microarrays. BMC Bioinformatics. 2008 Jan 29; 9: 67. https://doi.org/10.1186/1471-2105-9-67 PMID: 18230172
11. Edwards A. Venn diagrams for many sets. New Scientist, 1989; 121(1646): 51–6.
Об авторах
Н. М. БулановРоссия
Буланов Николай Михайлович, канд. мед. наук, ассистент кафедры внутренних, профессиональных болезней и ревматологии
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119991
+7 (919) 100-22-79
О. Б. Блюсс
Россия
Блюсс Олег Борисович, канд. физ.-мат. наук, доцент кафедры педиатрии и детских инфекционных болезней; старший преподаватель, Школа физики, астрономии и математики, Университет Хартфордшира.
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119991
Колледж-лейн, Хатфилд, AL10 9AB, Великобритания
Д. Б. Мунблит
Россия
Мунблит Даниил Борисович, PhD, профессор кафедры педиатрии и детских инфекционных болезней; Почетный старший преподаватель, Секция воспаления, регенерации и развития, Национальный институт сердца и легких, Медицинский факультет
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119991
Эксибишн-роуд, Южный Кенсингтон, Лондон, SW7 2BU, Великобритания
Т. В. Назаренко
Великобритания
Назаренко Татьяна Валерьевна, научный сотрудник, Институт женского здоровья (Женская онкология)
Гоуэр-стрит, Лондон, WC1E 6BT
Д. В. Бутнару
Россия
Бутнару Денис Викторович, канд. мед. наук, проректор по научной работе
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119991
М. Ю. Надинская
Россия
Надинская Мария Юрьевна, канд. мед. наук, доцент кафедры пропедевтики внутренних болезней, гастроэнтерологии и гепатологии
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119991
А. А. Заикин
Россия
Заикин Алексей Анатольевич, канд. физ.-мат. наук, заместитель директора Центра анализа сложных систем; профессор системной медицины, Институт женского здоровья и кафедра математики
ул. Трубецкая, д. 8, стр. 2, г. Москва, 119991
Гоуэр-стрит, Лондон, WC1E 6BT, Великобритания