Перейти к:
Базовые аспекты мета-анализа. Часть 1
https://doi.org/10.47093/2218-7332.2023.14.1.4-14
Аннотация
Мета-анализ – одно из понятий научной методологии. Он является частым, но не обязательным компонентом систематического обзора эмпирических исследований. Для проведения мета-анализа объединяются результаты нескольких научных исследований и осуществляется проверка одной или нескольких взаимосвязанных научных гипотез при помощи количественных (статистических) методов. Для такого анализа можно использовать либо первичные данные оригинальных исследований, либо обобщенные опубликованные (вторичные) результаты исследований, посвященные одной проблеме. Мета-анализ используется для получения оценки величины неизвестного эффекта, а также для сравнения результатов различных исследований, выявляет в них закономерности или другие взаимосвязи, а также возможные источники разногласий. Мета-анализы занимают высшую ступень достоверности в концепции доказательной медицины, поэтому их результаты считаются самым надежным источником доказательств. Понимание всех этапов проведения мета-анализа позволит научным сотрудникам грамотно анализировать результаты таких исследований, а также формулировать задачи при самостоятельном проведении мета-анализов. В настоящей статье читатель познакомится с такими ключевыми понятиями мета-анализа, как взвешенные эффекты, гетерогенность, различные типы используемых статистических моделей, а также научится работать с некоторыми видами графиков, получаемых в мета-анализах.
Ключевые слова
Список сокращений:
ДИ – доверительный интервал
неРКИ – нерандомизированное исследование
РКИ – рандомизированное контролируемое исследование
Многие оригинальные исследования имеют сходные цели и задачи, но при этом проводятся разными коллективами, с разными пациентами, по иным протоколам и в разные временные промежутки. Результаты таких исследований могут быть разнообразны и противоречивы, что затрудняет принятие клинических решений. Благодаря концепции доказательной медицины разработаны инструменты, позволяющие объединить результаты многочисленных исследований, в определенной мере различающихся между собой [1]. Проверяя гипотезы в разных популяциях, мы получаем бесценные данные о том, что: а) эффект прослеживается у разных групп (или, наоборот, есть только в конкретных группах); б) существует вариабельность эффекта. Большое количество сходных исследований, по сути, являются репликациями одного большого эксперимента. Соответственно большее количество репликаций повышает мощность и степень доверия к результатам.
Существуют несколько основных инструментов, чтобы вынести суждение о совокупных результатах неких единообразных исследований.
- Систематические обзоры. Систематические обзоры включают все исследования, которые возможно найти, соответствующие неким строгим критериям включения. Данные критерии включения направлены на соблюдение ряда стандартов, предъявляемых к планированию исследований, их проведению и стандартным операционным процедурам и результатам (например, исследования по артериальной гипертензии, где артериальное давление оценивалось в соответствии с международными рекомендациями по кардиологии; исследования определенной манипуляции в хирургии, которая выполнялась строго в соответствии с четкими рекомендациями международных ассоциаций).
- Мета-анализы. Главным отличием мета-анализа от систематических обзоров является не только рассмотрение результатов ряда исследований, но и количественная оценка их результатов. В самом деле, нам необходимо знать не только то, что препарат/вмешательство обладает эффектом, но и оценить размер этого эффекта, и широту его вариабельности.
В настоящей публикации мы затронем базовые аспекты проведения мета-анализов, что делается после того, как проведен литературный поиск и фактически проведена бóльшая часть работы для систематического обзора.
ВКЛЮЧЕНИЕ ИССЛЕДОВАНИЙ В МЕТА-АНАЛИЗ
Рекомендации PRISMA
Детальное описание критериев и процесса литературного поиска не является темой настоящей публикации, однако важно помнить, что любое создание систематического обзора состоит из ряда ступеней. Эти ступени объединены в стандартную схему, получившую название «диаграмма PRISMA» (Preferred Reporting Items for Systematic Reviews and Meta-Analyses, предпочтительные элементы отчетности для систематических обзоров и мета-анализов), по названию соответствующих рекомендаций [2] (рис. 1). [2] (рис. 1).
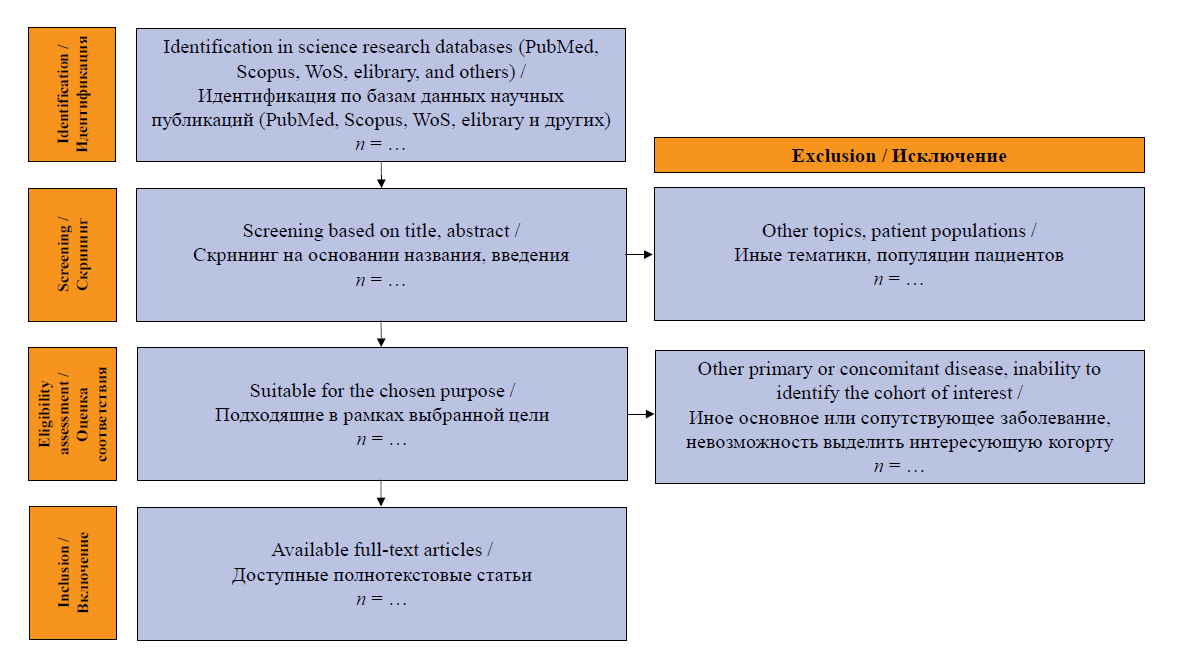
РИС. 1. Шаблон потоковой диаграммы PRISMA, адаптирована из M.J. Page и соавт. [2]
FIG. 1. PRISMA flow diagram template, adapted from M.J. Page et al. [2]
Собственно, мета-анализ начинается после того, как завершено включение и доступны исследования, из которых будет выполнена экстракция данных.
Основными рекомендациями по предварительным и дальнейшим шагам, представляющим для читателя практический интерес, являются:
- Руководство Кокрановского общества по составлению систематических обзоров (Cochrane Handbook for Systematic Reviews of Interventions)1 – данный документ размещен в интернете и представляет собой структурированное руководство с освещением практически всех аспектов литературного поиска, проведения метаанализа, базовых навыков по математической статистике, необходимых для такой работы.
- Рекомендации PRISMA, о которых мы упоминали выше [2].
Представленные рекомендации помогут соблюсти высокие стандарты при написании систематических обзоров и уменьшить число возможных ошибок и неточностей, которые впоследствии могут затруднить продолжение работы. В связи с тем что метаанализы широко используются фармацевтическими компаниями, а также иными коммерческими структурами, соблюдение указанных в рекомендациях стандартов проверяется рецензентами очень тщательно как при рассмотрении, так и при публикации статей. Строгое соблюдение регламента и рекомендаций является залогом успешной публикации.
ОЦЕНКА ВОЗМОЖНЫХ СМЕЩЕНИЙ В ПУБЛИКАЦИЯХ
После сбора всех подходящих публикаций для включения в систематический обзор или мета-анализ необходимо оценить их с точки зрения возможных смещений. К сожалению, источников потенциальных смещений может быть довольно много, поэтому были разработаны специальные инструменты, позволяющие исследователям проводить потенциальную оценку публикаций. Такие инструменты получили название графики риска смещений, или risk of bias plots.
Данные графики можно строить для исследований с различными типами дизайна, в первую очередь для рандомизированных контролируемых исследований (РКИ) (рис. 2) и для нерандомизированных исследований (неРКИ) [3] [ 4] (рис. 3). Графики, приведенные ниже, получили название «светофоры». Основная идея сводится к тому, что исследователи, проводящие мета-анализ с включением РКИ (рис. 2), рассматривают каждое исследование по отдельности и оценивают, насколько велики риски, ассоциированные с 5 доменами:
- рандомизацией;
- вмешательством;
- пропущенными данными;
- оценкой конечной точки;
- представлением результатов.
Риск оценивается как «высокий», «средний» и «низкий».
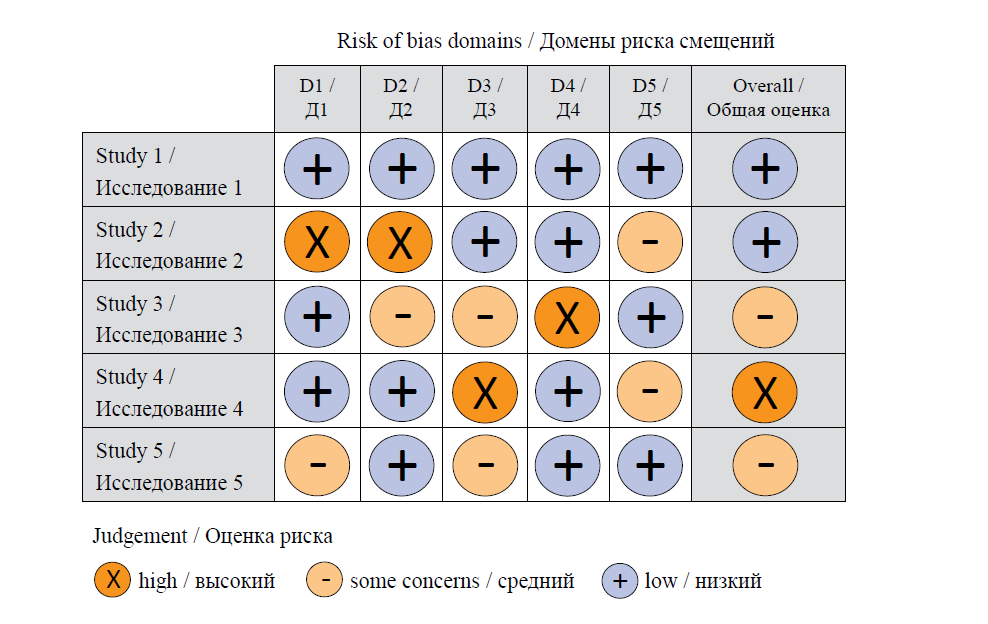
РИС. 2. Диаграмма светофор для рандомизированных контролируемых исследований, адаптирована из L.A. McGuinness
и соавт. [5]
FIG. 2. Traffic light plot for randomized controlled trials, adapted from L.A. McGuinness et al. [5]
Примечание: риск смещения, ассоциированный с доменами: Д1 – рандомизацией; Д2 – вмешательством; Д3 – пропущенными данными; Д4 –
оценкой конечной точки; Д5 – представлением результатов.
Note: risk of bias associated with the domains: D1 – randomization; D2 – deviations from intended interventions; D3 – missing data; D4 – measurement
of outcome; D5 – selection of reported results
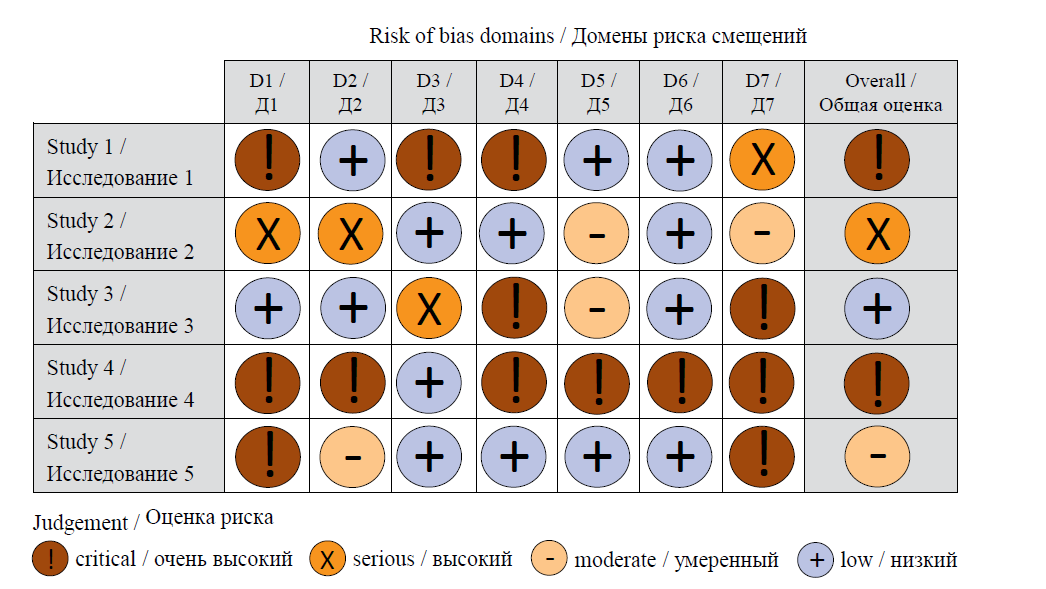
РИС. 3. Диаграмма светофор для когортных исследований, адаптирована из L.A. McGuinness и соавт. [5]
FIG. 3. Traffic light plot for cohort studies, adapted from L.A. McGuinness et al. [5]
Примечание: риск смещения, ассоциированный с доменами: Д1 – конфаундинг (влияние вмешивающихся факторов); Д2 – отбором и вклю-
чением пациентов; Д3 – вмешательством; Д4 – расхождением с протоколом; Д5 – пропущенными данными; Д6 – оценкой конечной точки;
Д7 – представлением результатов.
Note: risk of bias associated with the domains: D1 – confounding; D2 – selection of participants; D3 – classification of interventions; D4 – deviations from
intended interventions; D5 – missing data; D6 – measurement of outcome; D7 – selection of reported results
В случае если в мета-анализ включаются неРКИ, оцениваются риски, связанные с 7 доменами:
- конфаундингом (confounding, влияние вмешивающихся факторов);
- отбором и включением пациентов;
- вмешательством;
- расхождением с протоколом;
- пропущенными данными;
- оценкой конечной точки;
- представлением результатов.
Оценка риска интерпретируется как потенциально «низкая», «умеренная», «высокая» и «очень высокая». Данный инструмент позволяет критически подходить к полученным в мета-анализе результатам и рассматривать исследования с высоким риском смещения как менее надежные. Детальное описание возможностей данного инструмента приведено на специализированном сайте2.
РАЗМЕР ЭФФЕКТА В МЕТА-АНАЛИЗЕ
Исследования, объединенные в мета-анализе, обычно оценивают результаты по идентичной конечной точке. Данная оценка есть эффект, который был достигнут, или наблюдаемый эффект. Эффект традиционно обозначается греческой буквой «тета» θ, наблюдаемый эффект по каждому из k исследований обычно обозначается, как θk. Понятие эффекта, его размера и его оценки описано в нашей публикации о тестировании статистических гипотез [6].
Существуют две основные концепции, позволяющие описать и оценить эффект нескольких исследований. Обе эти концепции привязаны к соответствующим статистическим моделям с фиксированными и со случайными эффектами.
Модель с фиксированными эффектами
Эта модель подразумевает, что включенные в метаанализ исследования очень похожи друг на друга в отношении дизайна, количества пациентов, методологии проведения, оценки результатов и других параметров. Исследования представляются сходными настолько, что их результаты, или эффекты θ1,2,3,...k, считают единой выборкой из одной генеральной совокупности всех возможных аналогичных исследований.
Вероятностное распределение такой совокупности имеет математическое ожидание (среднее взвешенное по вероятностям возможных значений), представляющее собой некий истинный размер эффекта θ̂ . Соответственно каждое исследование представляет собой элемент совокупности, а несколько случайно взятых из такого распределения исследований (мета-анализ) представляют собой банальную выборку.
Наблюдаемый эффект в каждом исследовании k будет отличаться от истинного на величину ошибки:
θ̂ = θk + ϵk.
Соответственно мы считаем, что среди нескольких исследований наиболее точными являются те, где величина выборочной ошибки ϵ наименьшая (рис. 4).
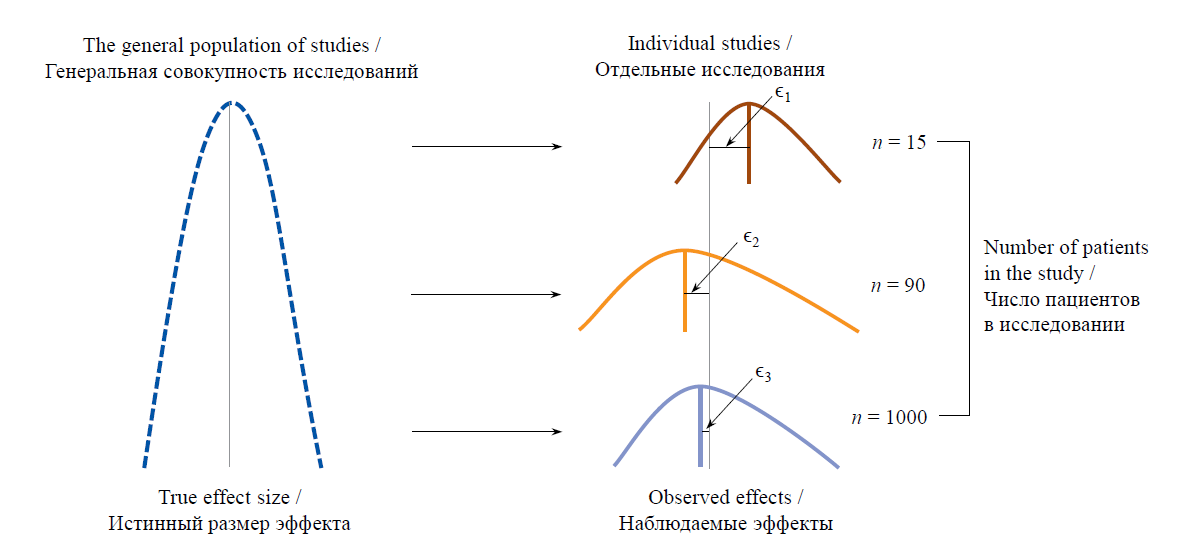
РИС. 4. Схематичное представление истинного и наблюдаемых эффектов в исследованиях при использовании модели
с фиксированными эффектами
FIG. 4. Schematic representation of true and observed effects in studies using a fixed effects model
Примечание: ϵk – величина выборочной ошибки; серая линия – истинный размер эффекта; цветные прямые линии – наблюдаемые эффекты.
Note: ϵk – sampling error; grey line – true effect size; colored straight lines – observed effects
Выборка из нескольких исследований {1,2,3,...k} должна иметь некую центральную тенденцию или математическое ожидание, отражающее истинный размер эффекта. Таким образом, используя определение математического ожидания как среднее взвешенное, получаем:
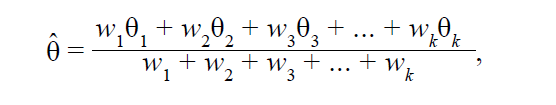
• θ̂ – взвешенный размер эффекта по k исследованиям, являющийся результатом мета-анализа;
• θk – наблюдаемый эффект исследования k;
• wk – вес исследования k.
Из данного уравнения неясным остается, как получить вес каждого исследования. Как мы знаем, наблюдаемый эффект, полученный в исследовании k, является точечной оценкой (point estimate). В исследование k включено определенное количество пациентов, n. Мерой вариабельности эффекта θk будет его стандартная ошибка, рассчитанная как:
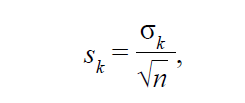
где
√n • σ – стандартное отклонение эффекта θk в исследовании k;
• n – количество пациентов в исследовании k.
В модели с фиксированными эффектами один из способов расчета весов выполняется с помощью так называемого метода обратной дисперсии (inverse variance method):
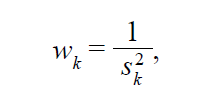
где
• sk 2 – квадрат стандартной ошибки эффекта θk в исследовании k;
• wk – вес исследования k.
Таким образом, в модели с фиксированными эффектами вес любого исследования обратно связан с величиной обратной ошибки эффекта в исследовании и напрямую – с количеством включенных в исследование пациентов. Допущением модели является тот факт, что ничто, кроме количества пациентов, не может влиять на вес исследования.
Данная концепция, с одной стороны, представляется излишне упрощенной. В реальном мире исследования так или иначе отличаются друг от друга и данные различия обусловлены огромным количеством факторов помимо размера выборки.
Модель со случайными эффектами
Если в мета-анализе объединены исследования различного дизайна (РКИ, когортные и т.п.), проведенные в разные годы, в разных странах, в центрах с разными стандартами оказания медицинской помощи, с протоколами вмешательств по разным клиническим рекомендациям, требуется модель, которая будет учитывать различия не только по объему выборки, но и по вышеупомянутым факторам.
Такая модель предполагает, что эффект по каждому исследованию, включенному в мета-анализ, является выборкой из собственной совокупности размеров эффекта и отличается от математического ожидания собственной совокупности на величину ϵk (рис. 5).
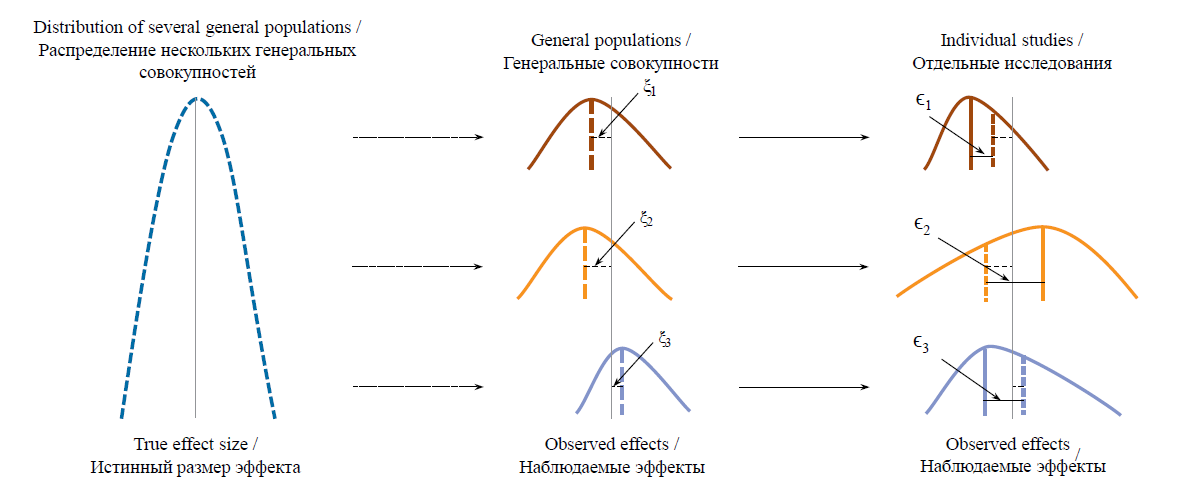
РИС. 5. Схематичное представление истинного и наблюдаемых эффектов в исследованиях при использовании модели со
случайными эффектами
FIG. 5. Schematic representation of true and observed effects in studies using a random effects model
Примечание: ξk – величина ошибки каждой генеральной совокупности; ϵk – величина выборочной ошибки; серая линия – истинный размер
эффекта; цветные пунктирные линии – наблюдаемые эффекты в генеральной совокупности; цветные прямые линии – в отдельных исследо-
ваниях.
Note: ξk – error of each general population; ϵk – sampling error; grey line – true effect size; colored dotted lines – observed effects in general populations;
colored straight lines – in individual studies.
Если мы включили в мета-анализ k исследований, следовательно, это k выборок из k различных генеральных совокупностей. При этом k совокупностей имеют свое распределение с математическим ожиданием в виде взвешенного размера эффекта, при этом каждая генеральная совокупность отличается от математического ожидания своего распределения на величину ξk. Такое общее распределение имеет точечную оценку, которая соответствует взвешенному эффекту в мета-анализе, θ̂, и дисперсию τ2.
Таким образом, точечная оценка эффекта в каждом исследовании среди k отличается от взвешенного эффекта следующим образом:
θ̂ = θk + ϵk + ξk.
Показатель ξk объединяет различия, которые не связаны с ошибкой выборки.
Модель, которая использует данную логику, получила название модель со случайными эффектами. Веса индивидуальных исследований в такой модели рассчитываются следующим образом:
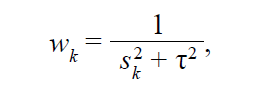
где
• sk 2 – квадрат стандартной ошибки эффекта θk в исследовании k;
• wk – вес исследования k;
• τ2 – дисперсия распределения нескольких генеральных совокупностей.
В свою очередь, взвешенный эффект рассчитывается абсолютно так же, как и для модели с фиксированными эффектами:
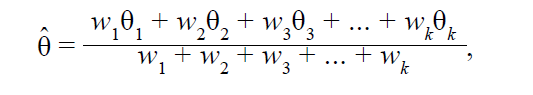
где • θ̂ – взвешенный размер эффекта по k исследованиям, являющийся результатом мета-анализа;
• θk – наблюдаемый эффект исследования k;
• wk – вес исследования k.
Для вычисления показателя τ2 используются различные математические подходы, наиболее часто – DerSimonian-Laird, ограниченного максимального правдоподобия (Restricted Maximum Likelihood), максимального правдоподобия (Maximum Likelihood), процедура Paule-Mandel и другие [7–9]. Выбор конкретного метода зависит от типа оценки конечной точки и от конкретной ситуации, поэтому требует консультации с биостатистиком.
HETEROGENEITY ASSESSMENT ОЦЕНКА ГЕТЕРОГЕННОСТИ
Мы выяснили, что включенные в мета-анализ исследования могут значительно различаться, более того, в зависимости от этих различий избирается та или иная модель анализа. Существует ли некая мера, с помощью которой можно оценивать степень различий? Можем ли мы как-то объяснить степень различий, и нужно ли это делать? Как определить, какие исследования больше отличаются от других? На все эти вопросы может дать ответ концепция о гетерогенности.
Гетерогенность зависит от многих причин, наиболее частые из которых:
- неверный подбор исследований для мета-анализа;
- наличие явных и скрытых факторов-модераторов, влияющих на взвешенный эффект (модератор фактически создает подгруппы с разным размером эффекта);
- небольшое количество исследований, используемых для мета-анализа.
Когда исследователи сталкиваются с избыточной гетерогенностью, например в ситуации, где у ряда исследований противоположное направление эффекта или когда крайне разный размер эффекта, необходимо разобраться, не имеет ли место ошибочное включение исследований в мета-анализ. Попытка объединить исследования, в которых оценивались совершенно разные параметры, приведет к огромной гетерогенности и не ответит на вопрос мета-анализа. Результаты такого мета-анализа будут крайне сомнительны.
Если мы считаем, что на данном этапе ошибки нет, необходимо далее искать причину высокой гетерогенности. Например, при использовании нестандартизованных показателей необходимо попытаться использовать стандартизованные. Ряд показателей может быть измерен в разных шкалах или значительно различаться на включении между исследованиями – стандартизация позволяет сгладить такие различия.
Следующей причиной высокой гетерогенности является наличие скрытых или явных модераторов или конфаундеров. Например, при оценке распространенности сердечно-сосудистых заболеваний явными модераторами являются пол и возрастная группа пациентов. Включение модератора и оценка его влияния на эффект и гетерогенность проводится с помощью метарегрессионного анализа, или метарегрессии. Дальнейший анализ подгрупп позволяет значительно снизить гетерогенность.
Наконец, малое количество исследований в метаанализе может привести к высокой гетерогенности.
По G. Rücker, существует 2 основных типа гетерогенности [10]:
- Гетерогенность, обусловленная дизайном или базовыми характеристиками. Причиной является попытка объединить в мета-анализе различные по дизайну исследования (включая тип исследования, характер вмешательства, способ оценки результатов, срок их оценки и другие параметры), а также исследования, сильно гетерогенные по когортам пациентов. Данный тип гетерогенности может приводить к статистической гетерогенности.
- Статистическая гетерогенность. Обусловлена точностью оценки и вариабельностью размера эффекта. Данную гетерогенность уже можно оценить количественно. Одной из причин (но совсем не всегда) статистической гетерогенности может быть гетерогенность, обусловленная дизайном. Methods to measure heterogeneity
Способы оценки гетерогенности
Cochran`s Q
Мы рассмотрели оба типа моделей и поняли, что существует наблюдаемый эффект θ̂ k некоего исследования k, а также взвешенный эффект, который мы рассчитываем θ̂ для всех исследований мета-анализа. Мы также помним, что у каждого исследования есть свой вес wk. Отклонение наблюдаемого эффекта от взвешенного может быть направлено в любую сторону (может быть с любым знаком). Если мы возведем отклонение в квадрат, оно больше не будет привязано к направлению.
Сумма взвешенных квадратов таких отклонений получила название Cochran’s Q:
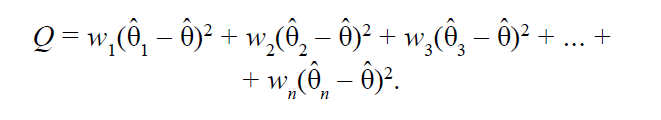
Мы можем рассчитать отклонение наблюдаемого эффекта от взвешенного по всем исследованиям.
Распределение Cochran’s Q сильно приближено к распределению χ2 с K – 1 степенями свободы, где K – количество исследований в мета-анализе.
Cochran’s Q будет расти при увеличении количества исследований в мета-анализе, а также при наличии в нем крупных исследований с большим количеством пациентов.
I2-статистика Хиггинса и Томпсона
Данная статистика рассчитывается с помощью Cochran’s Q и указывает на % гетерогенности, обусловленный ошибкой ξk (ошибкой, не связанной с размером выборки).
Нулевая гипотеза состоит в том, что гетерогенность отсутствует и Cochran’s Q следует распределению χ2 с K – 1 степенями свободы (ожидаемая гетерогенность). Но у нас имеется и наблюдаемая гетерогенность Q. Тогда отклонение наблюдаемой гетерогенности от ожидаемой составляет:
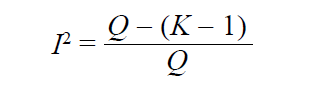
и выражается в долях единицы или в процентах.
Принято выделять низкую (до 25%), умеренную (25–75%) и высокую (75% и выше) гетерогенность [11].
H2-статистика
Данная статистика рассчитывает отношение Q-статистики к K – 1: при отсутствии гетерогенности значение стремится к 1. Более высокие значения говорят о наличии гетерогенности между исследованиями.
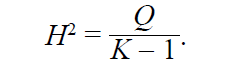
Дисперсия гетерогенности τ2
Истинный взвешенный эффект имеет собственную дисперсию τ2 и стандартное отклонение τ. Данная статистика хорошо подходит для оценки меры гетерогенности, имея ту же размерность, что и эффект в исследованиях в мета-анализе. Зная рассчитанный взвешенный размер эффекта θ̂ в мета-анализе, мы можем оценить 95% доверительный интервал (ДИ) истинного эффекта как θ̂ ± 1,96 × τ.
АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ
Анализ чувствительности показывает, какое влияние могут оказать отдельные исследования на взвешенный эффект, или, другими словами, насколько результаты мета-анализа устойчивы.
Одним из наиболее часто используемых способов оценки чувствительности является метод leave-one-out Каждое исследование по одному удаляется из мета-анализа, после чего размер взвешенного эффекта и гетерогенность пересчитываются. Серьезные изменения по величине размера эффекта и снижение гетерогенности указывают на то, что именно исключенное исследование оказывает существенное влияние на общий результат. Если первоначально такое исследование в графике-«светофоре» было оценено исследователями как обладающее высоким/умеренным риском смещения, оно может быть исследованием-выбросом, и необходимо рассматривать целесообразность его присутствия в мета-анализе.
Графически результаты анализа чувствительности представлены на рисунке 6.
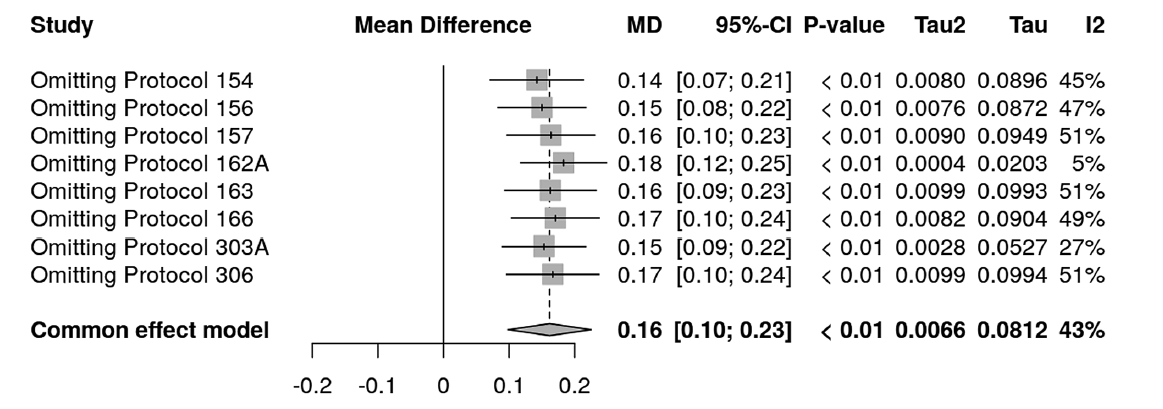
РИС. 6. Форест-диаграмма, демонстрирующая анализ чувствительности, адаптирована из S. Balduzzi и соавт. [12]
FIG. 6. Forest plot showing sensitivity analysis, adapted from S. Balduzzi et al. [12]
Примечание: study – исследование; MD – Mean difference, разница средних; Cl – confidence interval, доверительный интервал; P-value – значе-
ние p; I2 – Higgin’s & Thompson’s I2 statistic / I2 statistic, I2-статистика Хиггинса и Томпсона / I2-статистика; common (fixed) effect model – модель
с фиксированными эффектами.
Note: MD – Mean difference; Cl – confidence interval; I2 – Higgin’s & Thompson’s I2 statistic / I2 statistic.
В примере на рисунке 6 взвешенный эффект, полученный в мета-анализе, является разницей средних (mean difference) и составил 0,16 [0,1; 0,23], мы видим, что при исключении поочередно исследований из мета-анализа взвешенный эффект существенно не меняется. При этом исключение исследования Protocol 162A существенно снижает гетерогенность, по статистике I2 до 5%. Данное исследование требует пристального внимания, так как его присутствие обуславливает высокие значения гетерогенности во всем мета-анализе.
В общем случае анализ чувствительности направлен на оценку того, как меняется взвешенный эффект при исключении исследований, которым при оценке потенциальных рисков смещения был присвоен «высокий» и «очень высокий» уровень риска. При возникновении существенного влияния на эффект при исключении таких исследований (например, в ситуации, когда после исключения исследований с высоким риском 95% ДИ нового взвешенного эффекта перестает включать точечную оценку взвешенного эффекта до исключения исследований) необходимо пересмотреть необходимость включения исследований с высоким риском в мета-анализ
ФОРЕСТ-ДИАГРАММА (FOREST PLOT)
Наиболее общим способом суммировать результаты мета-анализа является форест-диаграмма (forest plot) – специфический график, отображающий исследования, вошедшие в анализ, эффект в каждом из них, взвешенный эффект, а также ряд дополнительных характеристик, например, веса каждого исследования, показатели гетерогенности, тип выбранной статистической модели (фиксированные или случайные эффекты). Неотъемлемой частью forest plot является диаграмма, дублирующая размеры эффекта и их 95% ДИ, а также взвешенный эффект и его 95% ДИ.
Довольно часто размер точек на графике, характеризующих определенное исследование, связан с весом данного исследования (соответственно, точки наибольшего размера связаны с исследованиями с наибольшим весом).
Типичный forest plot показан на рисунке 7. Данные исследования взяты из материалов, сопровождающих библиотеку meta языка программирования R [12].
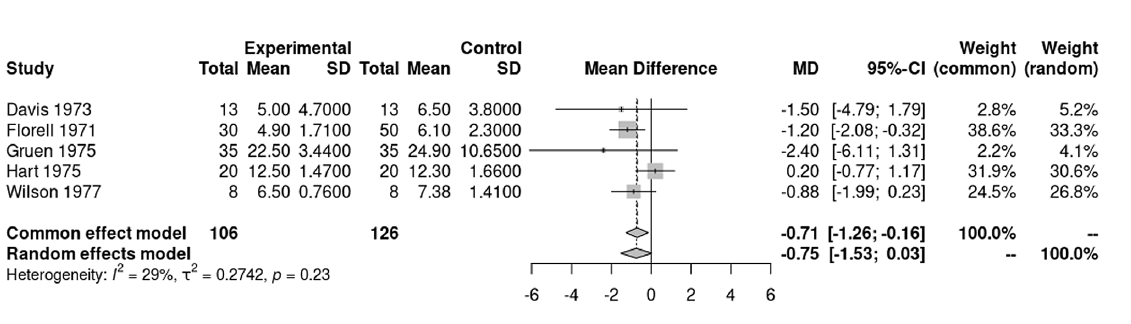
РИС. 7. Forest-диаграмма, демонстрирующая взвешенный эффект, адаптирована из S. Balduzzi и соавт. [12]
FIG. 7. Forest plot showing the weighted effect, adapted from S. Balduzzi et al. [12]
Примечание: study – исследование; experimental – экспериментальная группа; control – контрольная группа; total – общее значение; mean –
среднее значение; SD – standard deviation, стандартное отклонение; MD – mean difference, разница средних; CI – confidence interval, до-
верительный интервал; weight (common) – веса в модели с фиксированными эффектами; weight (random) – веса в модели со случайными
эффектами; common (fixed) effect model – модель с фиксированными эффектами; random effect model – модель со случайными эффектами;
heterogeneity – гетерогенность; I2 – Higgin’s & Thompson’s I2 statistic / I2 statistic, I2-статистика Хиггинса и Томпсона / I2-статистика; τ2 – Tausquared,
Тау-квадрат; P-value – значение p.
Note: SD – standard deviation; MD – mean difference; CI – confidence interval; I2 – Higgin’s & Thompson’s I2 statistic / I2 statistic; τ2 – Tau-squared.
На рисунке 7 мы видим названия исследований и год публикации результатов, характеристики основных и контрольных групп (количества, средние и стандартные отклонения – необходимые нам данные для расчета стандартной ошибки), размер эффекта (в данном случае разница средних, mean difference, MD) и его 95% ДИ, веса в моделях с фиксированными и случайными эффектами, взвешенный эффект для обоих типов моделей, а также показатели гетерогенности.
Также мы видим диаграмму с отрисовкой все тех же размеров эффекта в исследованиях (в виде квадратов, размер которых указывает на веса) и взвешенные эффекты для моделей с фиксированными и случайными эффектами (в виде ромбов).
Вертикальная сплошная черта обозначает размер эффекта, равный нулю. Так как мы имеем дело с разницей средних, если 95% ДИ отдельных исследований или взвешенных эффектов включает ноль, значит высока вероятность, что наблюдаемые точечные оценки случайны.
В настоящем примере единственное исследование, где наблюдается значимый эффект, – Florell 1971, его вес в модели как с фиксированными, так и со случайными эффектами наивысший (38,6 и 33,3% соответственно). По результатам мета-анализа модель с фиксированными эффектами показывает наличие значимого эффекта, разница средних составила -0,71 [-1,26; -0,16], при этом результаты модели со случайными эффектами оказались незначимыми: точечная оценка составила -0,75, а 95% ДИ включает ноль [-1,53; 0,03].
ЗАКЛЮЧЕНИЕ
В настоящей части статьи мы познакомились с этапами включения исследований в мета-анализ, рассмотрели существующие рекомендации, с которыми необходимо познакомиться при написании мета-анализа, детально разобрали процесс создания весов, различные типы моделей, используемых в мета-анализах. Также мы познакомились с понятием гетерогенности и способом ее вычисления. Были представлены основные графики, публикуемые в мета-анализах, такие как forest plot и график leave-oneout для анализа чувствительности. В следующей публикации мы рассмотрим, как происходит анализ подгрупп и концепцию метарегрессии, а также научимся оценивать публикационное смещение, визуально и математическими методами. Дополнительно мы вспомним, как наиболее часто оценивается эффект в мета-анализе, и остановимся на стандартизованных показателях и оценке для них стандартной ошибки.
Конфликт интересов. Авторы заявляют об отсутствии конфликта интересов.
Финансирование. Статья подготовлена при поддержке программы стратегического академического лидерства «Приоритет-2030» ФГАОУ ВО «Первый Московский государственный медицинский университет им. И.М. Сеченова» Минздрава России (Сеченовский Университет).
Conflict of interests. The authors declare that there is no conflict of interests.
Financial support. This article was supported by the Academic leadership program Priority 2030 proposed by Sechenov First Moscow State Medical University (Sechenov University)
1 Cochrane Handbook for Systematic Reviews of Interventions version 6.2 (updated February 2021). Cochrane, 2021. Available from https://training.cochrane.org/handbook/current
2 https://www.riskofbias.info/ (access date 01.11.2022).
Список литературы
1. Sackett D. L., Rosenberg W. M., Gray J. A., et al. Evidence based medicine: what it is and what it isn’t. BMJ. 1996 Jan 13; 312 (7023): 71–72. doi: 10.1136/bmj.312.7023.71. PMID: 8555924
2. Page M. J., McKenzie J. E., Bossuyt P. M., et al. The PRISMA 2020 statement: an updated guideline for reporting systematic reviews BMJ 2021; 372: n71. doi: 10.1136/bmj.n71
3. Sterne J. A. C., Savović J., Page M. J., et al. RoB 2: a revised tool for assessing risk of bias in randomised trials. BMJ. 2019 Aug 28; 366: l4898. doi: 10.1136/bmj.l4898. PMID: 31462531
4. Sterne J. A., Hernán M. A., Reeves B. C., et al. ROBINS-I: a tool for assessing risk of bias in non-randomised studies of interventions. BMJ. 2016 Oct 12; 355: i4919. doi: 10.1136/bmj.i4919. PMID: 27733354
5. McGuinness L. A., Higgins J. P. T. Risk-of-bias VISualization (robvis): An R package and Shiny web app for visualizing risk-of-bias assessments. Res Synth Methods. 2021 Jan; 12 (1): 55–61. doi: 10.1002/jrsm.1411. Epub 2020 May 6. PMID: 32336025
6. Suvorov A. Yu., Bulanov N. М., Shvedova A. N., et al. Statistical hypothesis testing: general approach in medical research. Sechenov Medical Journal. 2022; 13 (1): 4–13. doi: 10.47093/2218-7332.2022.426.08
7. Viechtbauer W. Bias and efficiency of meta-analytic variance estimators in the random-effects model. Journal of Educational and Behavioral Statistics, 2005; 30 (3): 261–293. doi: 10.3102/10769986030003261
8. Veroniki A. A, Jackson D., Viechtbauer W., et al. Methods to estimate the between-study variance and its uncertainty in meta-analysis. Res Synth Methods. 2016 Mar; 7 (1): 55–79. doi: 10.1002/jrsm.1164. Epub 2015 Sep 2. PMID: 26332144
9. Langan D., Higgins J. P. T., Jackson D., et al. A comparison of heterogeneity variance estimators in simulated random-effects meta-analyses. Res Synth Methods. 2019 Mar; 10 (1): 83–98. doi: 10.1002/jrsm.1316. Epub 2018 Sep 6. PMID: 30067315
10. Rücker G., Schwarzer G., Carpenter J. R., Schumacher M. Undue reliance on I(2) in assessing heterogeneity may mislead. BMC Med Res Methodol. 2008 Nov 27; 8: 79. doi: 10.1186/1471-2288-8-79. PMID: 19036172
11. Higgins J. P., Thompson S. G. Quantifying heterogeneity in a meta-analysis. Stat Med. 2002 Jun 15; 21 (11): 1539–1558. doi: 10.1002/sim.1186. PMID: 12111919
12. Balduzzi S., Rücker G., Schwarzer G. How to perform a meta-analysis with R: a practical tutorial. Evid Based Ment Health. 2019 Nov; 22 (4): 153–160. doi: 10.1136/ebmental-2019-300117. Epub 2019 Sep 28. PMID: 31563865
Об авторах
А. Ю. СуворовРоссия
Александр Юрьевич Суворов, канд. мед. наук, главный статистик
Центр анализа сложных систем
119991
ул. Трубецкая, д. 8, стр. 2
Москва
И. В. Латушкина
Россия
Ирина Викторовна Латушкина, младший научный сотрудник
Центр анализа сложных систем
119991
ул. Трубецкая, д. 8, стр. 2
Москва
Тел.: +7 (916) 126-12-85
К. А. Гуляева
Россия
Ксения Александровна Гуляева, аспирант
кафедра пропедевтики внутренних болезней, гастроэнтерологии и гепатологии
119991
ул. Трубецкая, д. 8, стр. 2
Москва
Н. М. Буланов
Россия
Николай Михайлович Буланов, канд. мед. наук, доцент
кафедра внутренних, профессиональных болезней и ревматологии
119991
ул. Трубецкая, д. 8, стр. 2
Москва
М. Ю. Надинская
Россия
Мария Юрьевна Надинская, канд. мед. наук, доцент
кафедра пропедевтики внутренних болезней, гастроэнтерологии и гепатологии
119991
ул. Трубецкая, д. 8, стр. 2
Москва
А. А. Заикин
Россия
Алексей Анатольевич Заикин, канд. физ-мат. наук, заместитель директора
Центр анализа сложных систем
119991
ул. Трубецкая, д. 8, стр. 2
Москва